
 如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.
如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.分析 (Ⅰ)运用椭圆的定义,可得|AF1|+|AF2|=|BF2|+|BF1|=2a,可得4a=8,解得a=2,再由a,b,c的关系,可得b,进而得到椭圆的方程;
(Ⅱ)设直线AB:y=kx-1与椭圆的交点A(x1,y1),B(x2,y2),C(-x1,y1),D(-x2,y2),代入椭圆方程,运用韦达定理和弦长公式,化简整理,再由基本不等式即可得到S的最大值;
(Ⅲ)依题意可知AD与BC的交点在y轴上,求出直线BC:$\frac{y-{y}_{2}}{x-{x}_{2}}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}+{x}_{1}}$,令x=0,代入韦达定理,化简整理,可得y=-4,即可得到定点.
解答 解:(Ⅰ)依题意可知|AF2|+|BF2|+|AB|=8,
由椭圆的定义可得|AF1|+|AF2|=|BF2|+|BF1|=2a,
可得4a=8,解得a=2,
又c=1,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则椭圆方程为$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1;
(Ⅱ)设直线AB:y=kx-1与椭圆的交点A(x1,y1),B(x2,y2),C(-x1,y1),D(-x2,y2),
根据对称性,不妨设k>0,x1<0<x2,y2>y1,
由$\left\{\begin{array}{l}{y=kx-1}\\{3{y}^{2}+4{x}^{2}=12}\end{array}\right.$得:(4+3k2)x2-6kx-9=0,
得△=36k2+36(3k2+4)>0,x1+x2=$\frac{6k}{4+3{k}^{2}}$,x1x2=-$\frac{9}{4+3{k}^{2}}$,
S=2${S}_{△A{F}_{2}D}$=2•$\frac{1}{2}$•$\sqrt{1+{k}^{2}}$|x1|•$\frac{|-k{x}_{2}-{y}_{2}-1|}{\sqrt{1+{k}^{2}}}$
=2|k|•|x1x2|=$\frac{18|k|}{4+3{k}^{2}}$=$\frac{18}{3|k|+\frac{4}{|k|}}$≤$\frac{3\sqrt{3}}{2}$,
当且仅当|3k|=$\frac{4}{|k|}$,即k=±$\frac{2\sqrt{3}}{3}$时,取到最大值$\frac{3\sqrt{3}}{2}$;
(Ⅲ)证明:依题意可知AD与BC的交点在y轴上,
直线BC:$\frac{y-{y}_{2}}{x-{x}_{2}}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}+{x}_{1}}$,令x=0,
得y=$\frac{-{x}_{2}({y}_{2}-{y}_{1})}{{x}_{1}+{x}_{2}}$+y2=$\frac{2k{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}}$,
代入x1+x2=$\frac{6k}{4+3{k}^{2}}$,x1x2=-$\frac{9}{4+3{k}^{2}}$,
可得y=-4,
所以直线AD与BC的交点为(0,-4).
点评 本题考查椭圆的方程的求法,注意运用定义法,考查三角形的面积的最值的求法,注意运用联立直线方程和椭圆方程,运用韦达定理和弦长公式,以及基本不等式,考查直线恒过定点的问题的解法,注意运用直线方程,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
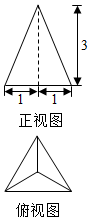
| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com