
分析 (1)设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0),由题意利用椭圆定义及性质求出a,b,由此能求出椭圆C的方程.
(2)由题意知直线PB的斜率k(k≠0)存在,直线PB的方程为y=k(x-3),与椭圆联立得到(2+3k2)x2-18k2x+27k2-6=0,由此利用根的判别式、韦达定理、直线斜率,结合题设条件能求出直线AE与x轴相交于定点(1,0).
解答 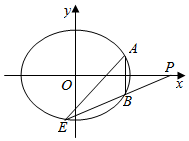 解:(1)设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
解:(1)设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
由题意,2a=|QF1|+|QF2|=$\sqrt{{2}^{2}+(\frac{2}{\sqrt{3}})^{2}}$+$\frac{2}{\sqrt{3}}$=2$\sqrt{3}$,…(2分)
解得a=$\sqrt{3}$,b2=a2-c2=3-1=2.
故椭圆C的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.…(4分)
(2)由题意知直线PB的斜率k(k≠0)存在,直线PB的方程为y=k(x-3).
设B(x1,y1),E(x2,y2).由题意A(x1,-y1),
由$\left\{\begin{array}{l}{y=k(x-3)}\\{\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y得:(2+3k2)x2-18k2x+27k2-6=0,…(6分)
由题意,判别式△=(-18k2)2-4(2+3k2)(27k2-6)>0,
由韦达定理,得${x}_{1}+{x}_{2}=\frac{18{k}^{2}}{2+3{k}^{2}}$,${x}_{1}{x}_{2}=\frac{27{k}^{2}-6}{2+3{k}^{2}}$,…(7分)
若直线AE与x轴相交于定点M(m,0),则A(x1,-y1)、M(m,0)、E(x2,y2)三点共线.
从而kAM=kAE,即$\frac{{y}_{1}}{m-{x}_{1}}$=$\frac{{y}_{1}+{y}_{2}}{{x}_{2}-{x}_{1}}$,…(8分)
解得m=$\frac{({x}_{2}-{x}_{1}){y}_{1}}{{y}_{1}+{y}_{1}}$+x1=$\frac{{x}_{2}{y}_{1}+{x}_{1}{y}_{2}}{{y}_{2}+{y}_{1}}$,…(9分)
∴$m=\frac{{x}_{2}{y}_{1}+{x}_{1}{y}_{2}}{{y}_{2}+{y}_{1}}$=$\frac{{x}_{2}•k({x}_{1}-3)+{x}_{1}•k({x}_{2}-3)}{k({x}_{2}-3)+k({x}_{1}-3)}$=$\frac{2{x}_{2}{x}_{1}-3({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-6}$…(11分)
=$\frac{2•\frac{27{k}^{2}-6}{2+3{k}^{2}}-3•\frac{18{k}^{2}}{2+3{k}^{2}}}{\frac{18{k}^{2}}{2+3{k}^{2}}-6}$=1.…(13分)
∴直线AE与x轴相交于定点(1,0).…(14分)
点评 本题考查椭圆方程的求法,考查直线与x轴交点坐标的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、直线斜率等知识点的合理运用.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
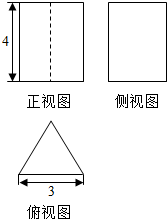
| A. | 36 | B. | 36$+\frac{9\sqrt{3}}{4}$ | C. | 36$+\frac{9\sqrt{3}}{2}$ | D. | 18$+\frac{9\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
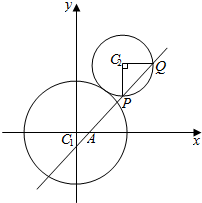 已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.
已知圆C1:x2+y2=9与圆C2:(x-3)2+(y-4)2=r2(r>0)相外切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.
如图,已知F1(0,-1),F2(0,1)为椭圆Γ:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点,过F1作两条倾斜角互补的直线l1,l2,l1,l2分别与椭圆Γ相交于A,B,C,D四点,且△ABF2的周长为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
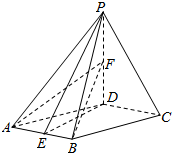 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,$\overline{x_1}$,$\overline{x{\;}_2}$分别表示甲、乙两名运动员这项测试成绩的平均数,$S_1^2$,$S_2^2$分别表示甲、乙两名运动员这项测试成绩的方差,则有( )| A. | $\overline{x_1}$>$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ | B. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$>$S_2^2$ | ||
| C. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$=$S_2^2$ | D. | $\overline{x_1}$=$\overline{x{\;}_2}$,$S_1^2$<$S_2^2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com