
分析 (1)根据函数成立的条件即可求函数f(x)的定义域;
(2)根据对数的运算性质,以及符合函数的值域的求法,即可得到答案,需要分类讨论.
解答 解:(1)要使函数有意义,则$\left\{\begin{array}{l}{-x-1>0}\\{x+3>0}\end{array}\right.$.
解得:-3<x<-1.
即f(x)的为定义域(-3,-1),
(2)f(x)=loga(-x-1)+loga(x+3)=loga[-(x+1)(x+3)],
令t=-(x+1)(x+3),
∵-3<x<-1,
∴0<t≤1,
当0<a<1时,值域为[0,+∞),
当a>1时,值域为(-∞,0].
点评 本题主要考查对数函数性质的综合考查,根据对数函数的单调性是解决本题的关键.注意要对a进行分类讨论.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
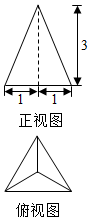
| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
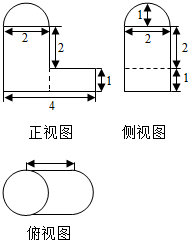
| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}})$ | C. | $[{-\frac{{\sqrt{6}}}{2},\frac{{\sqrt{6}}}{2}}]$ | D. | $[{-\frac{{2\sqrt{3}}}{3},\frac{{2\sqrt{3}}}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
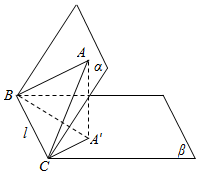 如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.
如图,已知二面角α-BC-β的大小为θ(0≤θ≤$\frac{π}{2}$).在面α内有△ABC,它在面β内的射影为△A′BC.它们的面积分别为S,S′,求证:cosθ=$\frac{S′}{S}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com