
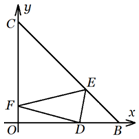
 如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$. 分析 根据题意,建立直角坐标系,写出对应点的坐标与直线方程,利用光的反射原理和对称性,求出点E、F的坐标,再计算|DE|、|EF|和|DF|的值,求和即可.
解答  解:建立如图所示的直角坐标系,由OB=3,BD=1,
解:建立如图所示的直角坐标系,由OB=3,BD=1,
可得B(3,0),C(0,3),D(2,0),∴BC的方程为x+y-3=0.
设M,N分别是点D关于直线BC和y轴的对称点,
则M(3,1),N(-2,0),
由光的反射原理可知,M,E,F,N四点共线,
又直线MN的方程为 $\frac{y-1}{0-1}$=$\frac{x-3}{-2-3}$,即 x-5y+2=0,
可得点E($\frac{13}{6}$,$\frac{5}{6}$),F(0,$\frac{2}{5}$),
∴|DE|=$\sqrt{{(\frac{13}{6}-2)}^{2}{+(\frac{5}{6}-0)}^{2}}$=$\frac{\sqrt{26}}{6}$,|EF|=$\sqrt{{(\frac{13}{6}-0)}^{2}{+(\frac{5}{6}-\frac{2}{5})}^{2}}$=$\frac{13\sqrt{26}}{30}$,
|DF|=$\sqrt{{(2-0)}^{2}{+(0-\frac{2}{5})}^{2}}$=$\frac{2\sqrt{26}}{5}$;
∴|DE|+|EF|+|DF|=$\sqrt{26}$,
故答案为:$\sqrt{26}$.
点评 本题考查求直线的方程,三角形的性质和轴对称图形的灵活应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | ab>ac | C. | a-|c|>b-|c| | D. | $\frac{1}{a}<\frac{1}{b}<\frac{1}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 1 | C. | $\sqrt{19}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com