
���� �������ָ��R2���̻��ع�Ч��ʱ��R2Խ��ģ�͵����Ч��Խ�ã�
�ڸ����س�����ķ�ȫ�����⣬д��P�ķVP���ɣ�
�۸�����̬�ֲ�N��0��1�������ʣ���P��X��1��=p���P��-1��X��0����ֵ��
�ܻع�ֱ��һ��������������ģ�$\overline{x}$��$\overline{y}$����
��� �⣺���ڢ٣������ָ��R2���̻��ع�Ч��ʱ��
R2Խ��˵��ģ�͵����Ч��Խ�ã���ٴ���
���ڢڣ�����P����?x0��R��x02-x0-1��0���ķ���
�VP����?x��R��x2-x-1��0��������ȷ��
���ڢۣ�������̬�ֲ�N��0��1�������ʿɵã�
��P��X��1��=p����P��X��-1��=p��
��P��-1��X��1��=1-2p��
��P��-1��X��0��=$\frac{1}{2}$-p������ȷ��
���ڢܣ��ع�ֱ��һ��������������ģ�$\overline{x}$��$\overline{y}$������ȷ��
���ϣ���ȷ��˵���Ǣڢۢܣ�
�ʴ�Ϊ���ڢۢܣ�
���� ���⿼���˸�����ͳ�Ƶ�Ӧ�����⣬Ҳ�������س�����ķ����⣬���ۺ��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{85}{2}$ | B�� | 32 | C�� | 64 | D�� | 31 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
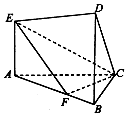 ����ͼ��ʾ�ļ������У�EA��ƽ��ABC��DB��EA��AC��BC����BC=BD=3��AE=2��AC=3$\sqrt{2}$��AF=2FB
����ͼ��ʾ�ļ������У�EA��ƽ��ABC��DB��EA��AC��BC����BC=BD=3��AE=2��AC=3$\sqrt{2}$��AF=2FB�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com