
设正整数构成的数列{an}使得a10k﹣9+a10k﹣8+…+a10k≤19对一切k∈N*恒成立.记该数列若干连续项的和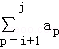 为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
为S(i,j),其中i,j∈N*,且i<j.求证:所有S(i,j)构成的集合等于N*.
见解析
【解析】
试题分析:显然S(i,j)∈N*,证明对任意n0∈N*,存在S(i,j)=n0.考虑10n0+10个前n项和,再考虑如下10n0+10个正整数:S1+n0<S2+n0<…<S10n0+10+n0,由抽屉原理,必有两个相等,可得结论.
证明:显然S(i,j)∈N*. (2分)
下证对任意n0∈N*,存在S(i,j)=n0.
用Sn表示数列{an}的前n项和,考虑10n0+10个前n项和:S1<S2<…<S10n0+10,(1)
由题设S10n0+10=(a1+a2+…+a10)+(a11+a12+…+a20)+…+(a10n0+1+a10n0+2+…+a10n0+10) (6分)
另外,再考虑如下10n0+10个正整数:S1+n0<S2+n0<…<S10n0+10+n0,(2)
显然S10n0+10+n0≤20n0+19 (10分)
这样(1),(2)中出现20n0+20个正整数,都不超过20n0+19,
由抽屉原理,必有两个相等.
由于(1)式中各数两两不相等,(2)式中各数也两两不等,
故存在i,j∈N*,使得Sj=Si+n0,即j>i,且n0=Sj﹣Si=S(i,j).
所以,所有S(i,j)构成的集合等于N*. (16分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:选择题
(4分)设点A(﹣2,3),B(3,2),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是( )
A.(﹣∞,﹣ ]∪[
]∪[ ,+∞) B.(﹣
,+∞) B.(﹣ ,
,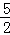 )
)
C.[﹣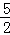 ,
, ] D.(﹣∞,﹣
] D.(﹣∞,﹣ ]∪[
]∪[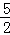 ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
已知x,y,z均为正数,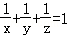 ,则
,则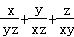 的最小值是( )
的最小值是( )
A.1 B.3 C. D.
D.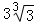
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
在半径为0.5m的圆桌中心上方安装一吊灯,桌面上灯光的强度y=k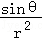 ,其中k是常数,r是灯与桌面上被照点的距离,θ是光线与桌面的夹角,为使桌边最亮,则sinθ=( )
,其中k是常数,r是灯与桌面上被照点的距离,θ是光线与桌面的夹角,为使桌边最亮,则sinθ=( )
A. B.
B. C.
C.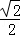 D.
D.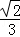
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.4绝对值的三角不等式练习卷(解析版) 题型:填空题
(2011•自贡三模)已知函数f(x)=|x﹣4|+|x+2|(x∈R且x≠0)的最小值为k则(2x﹣ )k的展开式的常数项是 (用数字作答)
)k的展开式的常数项是 (用数字作答)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷(解析版) 题型:选择题
(2014•南昌模拟)对任意x∈R,且x≠0,不等式|x+ |>|a﹣5|+1恒成立,则实数a的取值范围是( )
|>|a﹣5|+1恒成立,则实数a的取值范围是( )
A.(﹣∞,4)∪(6,+∞) B.(2,8) C.(3,5) D.(4,6)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•黄冈模拟)已知对任意m∈R,直线x+y+m=0都不是f(x)=x3﹣3ax(a∈R)的切线,则a的取值范围是( )
A.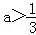 B.
B. C.
C.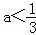 D.
D.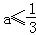
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com