练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．今年春节期间，在为期5天的某民俗庙会上，某摊点销售一种儿童玩具的情况如表：
    日期2月13日2月14日2月15日2月16日2月17日
    天气小雨小雨阴阴转多云多云转阴
    销售量上午4247586063
    下午5556626567
    由表可知：两个雨天的平均销售量为100件/天，三个非雨天的平均销售量为125件/天．
    （1）以十位位数字为茎，个位数字为叶．画出表中10个销售数据的茎叶图，并求出这组数据的中位数
    （2）假如明年庙会5天中每天下雨的概率为$\frac{2}{5}$，且每天下雨与否相互独立，其它条件不变．试估计庙会期间同一类型摊点能够售出的同种儿童玩具的件数；
    （3）已知摊位租金为1000元/个，该种玩具进货价为9元/件，售价为13元/件，未售出玩具可按进货价退回厂家，若所获利润大于1200元的概率超过0.6，则成为“值得投资”，那么在（2）的条件下，你认为“值得投资”吗？

    分析 （1）根据表中10个销售数据，可得茎叶图，从而求出这组数据的中位数；
    （2）设明年花市期间下雨天数为X，则X～B（5，$\frac{2}{5}$），估计明年花市可能有2天为下雨天，3天为非雨天，即可得出结论；
    （3）利润大于1200元时x的取值为575或600，求出相应的概率，即可得出结论

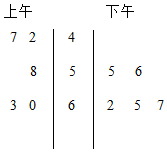    解答 解：（1）茎叶图如图所示，所有的数据为42，47，55，56，58，60，62，93，65，67，中位数=$\frac{1}{2}$（58+60）=59
    （2）设明年花市期间下雨天数为X，则X～B（5，$\frac{2}{5}$），
    ∴E（X）=5×$\frac{2}{5}$=2，
    ∴估计明年花市可能有2天为下雨天，4天为非雨天，
    ∴估计庙会期间同一类型摊点能够售出的同种儿童玩具的件数2×100+3×125=575件；
    （3）设民俗庙会获得利润为y元销售的件数为x，则y=4x-1000，
    由于y＞1200，
    得4x-1000＞1200，得x＞550，
    ∴利润大于1200元时x的取值为575或600，
    由（2），P（x=575）+P（x=600）=C52（$\frac{2}{5}$）2（$\frac{3}{5}$）3+C51（$\frac{2}{5}$）1（$\frac{3}{5}$）4=$\frac{162}{625}$+$\frac{216}{625}$＞0.6
    ∴在（2）条件下，认为“值得投资”．

    点评 本题考查了茎叶图的应用问题，考查了中位数的计算问题，考查概率的计算，考查学生分析解决问题的能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知F1、F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点．过F2作双曲线的渐近线的垂线，垂足为P，则|PF1|2-|PF2|2=（　　）
    A．4a2B．4b2C．3a2+b2D．a2+3b2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知$\overrightarrow{a}$=（$\sqrt{3}$sinωx，1），$\overrightarrow{b}$=（cosωx，0），其中ω＞0，又函数f（x）=$\overrightarrow{b}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）+k是以$\frac{π}{2}$为最小正周期的周期函数，当x∈[0，$\frac{π}{4}$]时，函数f（x）的最小值为-2
    （1）求f（x）的解析式；
    （2）写出函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在△ABC中，已知0＜A≤$\frac{π}{4}$，$\overrightarrow{AC}•\overrightarrow{BC}$=0，设$\overrightarrow{m}$=（cosA，cosB），$\overrightarrow{n}$=（sin2A，1+cos2B），$\overrightarrow{p}$=（cosC，sinC），现定义f（A）=|$\overrightarrow{n}$|-（$\overrightarrow{m}+\overrightarrow{n}$）$•\overrightarrow{p}$．
    （1）向量$\overrightarrow{m}$，$\overrightarrow{n}$是否一定共线？为什么？
    （2）试分别求出函数f（A）的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设i是虚数单位，复数z满足（1+i）z=2i50，则z的共轭复数$\overline{z}$为（　　）
    A．1+iB．1-iC．-1+iD．-1-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在△ABC中，角A、B、C所对的边分别为a、b、c，若b=2，△ABC的面积S=2$\sqrt{3}$，且2ccosA=2b-$\sqrt{3}$a，则a=4$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知数列{an}的前n项和为Sn=n2+2n，在等比数列{bn}中，b1+b3=5．b4+b6=40．
    （1）求数列{an}和{bn}的通项公式；
    （2）令cn=$\left\{\begin{array}{l}{\frac{2}{{S}_{n}}，n为奇数}\\{{b}_{n}，n为偶数}\end{array}\right.$，设数列{cn}的前n项和为Tn，求T2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知实数x，y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$，若z=x+ay的最大值是2，则实数a=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1（a＞0，b＞0）$的离心率为$\sqrt{5}$，则该双曲线的渐近线方程为（　　）
    A．y=±2xB．$y=±\frac{1}{2}x$C．$y=±\frac{1}{4}x$D．y=±4x

    查看答案和解析>>

    同步练习册答案