

| A. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | B. | f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$$<x<\frac{π}{2}$) | ||
| C. | f(x)=$\frac{|x|}{x}$ | D. | f(x)=x2ln(x2+1) |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)+f(-x)=0,即函数f(x)为奇函数②f(x)存在零点,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
解答 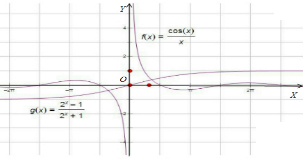 解:∵A,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,既是奇函数,而且函数图象与x也有交点,①符合题意;
解:∵A,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,既是奇函数,而且函数图象与x也有交点,①符合题意;
而B:f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$$<x<\frac{π}{2}$,x≠0)是奇函数,但函数图象与x无有交点,故不满足条件②;
而C:f(x)=$\frac{|x|}{x}$的函数图象与x轴没有交点,故不满足条件②;
而D:f(x)=x2ln(x2+1)明显不是奇函数,故不满足条件①;
故选:A.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2或$\frac{8}{3}$ | C. | 2或6 | D. | 2或8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值9 | B. | 有最大值9 | C. | 有最大值1 | D. | 有最小值1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com