练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若a>0，b>0，则p＝(ab)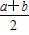，q＝ab·ba的大小关系是________．


    p≥q

    [解析]　∵a>0，b>0，∴p＝(ab)>0，q＝ab·ba>0，

    ＝＝a·b＝.

    若a>b，则>1，>0，∴>1；

    若a<b，则0<<1，<0，∴>1；

    若a＝b，则＝1，＝0，∴＝1.

    ∴≥1，即≥1.∵q>0，∴p≥q.

    [点评]　可运用特值法，令a＝1，b＝1，则p＝1，q＝1，有p＝q；

    令a＝2，b＝4，有p＝83＝512，q＝24×42＝256，∴p>q，故填p≥q.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示，在矩形ABCD中，AE⊥BD于E，S矩形＝40cm2，S△ABES△DBA＝15，则AE的长为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，圆ρ＝4cosθ的圆心C到直线ρsin(θ＋)＝2的距离为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标系中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，设曲线C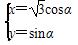：(α为参数)，直线l：ρ(cosθ＋sinθ)＝4.

    (1)写出曲线C的普通方程和直线l的直角坐标方程；

    (2)求曲线C上的点到直线l的最大距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＋b＝2，b>0，则＋的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式|2x＋1|＋|x－1|<2的解集为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a、b、c为正数，且a＋2b＋3c＝13，则＋＋的最大值为(　　)

    A.　　　                                                 B.　 　

    C.　　                                                  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出如下三个命题：

    ①四个非零实数a、b、c、d依次成等比数列的充要条件是ad＝bc；

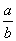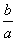    ②设a，b∈R，且ab≠0，若<1，则>1；

    ③若f(x)＝log2x，则f(|x|)是偶函数．

    其中不正确命题的序号是(　　)

    A．①②                                                        B．②③

    C．①③                                                        D．①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


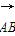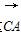    在复平面内，向量对应的复数是2＋i，向量对应的复数是－1－3i，则向量对应的复数为(　　)

    A．1－2i                                                       B．－1＋2i

    C．3＋4i                                                       D．－3－4i

    查看答案和解析>>

    同步练习册答案