
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,则下列结论中正确的个数是( )
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,则下列结论中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在①中,由EF∥BD,能推导出EF∥平面ABCD;在②中,连接BD,由AC⊥BD,AC⊥DD1,可知AC⊥面BDD1B1,从而得到面ACF⊥平面BEF;在③中,三棱锥E-ABF的体积与三棱锥A-BEF的体积相等,从而三棱锥E-ABF的体积为定值;在④中,令上底面中心为O,得到存在某个位置使得异面直线AE与BF成角30°.
解答 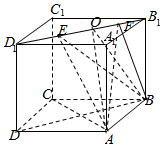 解:由正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,知:
解:由正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{{\sqrt{2}}}{2}$,知:
在①中,由EF∥BD,且EF?平面ABCD,BD?平面ABCD,得EF∥平面ABCD,故①正确;
在②中,连接BD,由AC⊥BD,AC⊥DD1,可知AC⊥面BDD1B1,
而BE?面BDD1B1,BF?面BDD1B1,∴AC⊥平面BEF,
∵AC?平面ACF,∴面ACF⊥平面BEF,故②正确;
在③中,三棱锥E-ABF的体积与三棱锥A-BEF的体积相等,
三棱锥A-BEF的底面积和高都是定值,故三棱锥E-ABF的体积为定值,故③正确;
在④中,令上底面中心为O,当E与D1重合时,此时点F与O重合,
则两异面直线所成的角是∠OBC1,可求解∠OBC1=300,
故存在某个位置使得异面直线AE与BF成角30°,故④正确.
故选:D.
点评 本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (-4,2) | ||
| C. | $({\frac{5}{2}_{\;}}{,_{\;}}4)$ | D. | $(-{∞_{\;}}{,_{\;}}\frac{5}{2})∪({4_{\;}}{,_{\;}}+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x±y=0 | B. | 4x±3y=0 | C. | 3x±4y=0 | D. | x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,中心为O,若椭圆过点P(-$\frac{1}{2}$,$\frac{1}{2}$),且AP⊥PO.
设椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,中心为O,若椭圆过点P(-$\frac{1}{2}$,$\frac{1}{2}$),且AP⊥PO.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com