
分析 根据已知条件∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}$∠BAC,得到OA=OC,
设∠BAC=α,∠ABC=β,∠ACB=γ,由正弦定理得:$\frac{OA}{sin(β-\frac{1}{2}α)}=\frac{BO}{sin\frac{1}{2}α}$,$\frac{CO}{sin\frac{1}{2}α}=\frac{BO}{sin(γ-\frac{1}{2}α)}$,两列相比得到:$si{n}^{2}\frac{1}{2}α$=sin(β-$\frac{1}{2}$α)•sin(γ-$\frac{1}{2}$α),化简后即可得到结论.
解答 证明:根据已知条件∠BAO=∠CAO=∠CBO=∠ACO=$\frac{1}{2}$∠BAC,
∴OA=OC,
设∠BAC=α,∠ABC=β,∠ACB=γ,
由正弦定理得:$\frac{OA}{sin(β-\frac{1}{2}α)}=\frac{BO}{sin\frac{1}{2}α}$,
$\frac{CO}{sin\frac{1}{2}α}=\frac{BO}{sin(γ-\frac{1}{2}α)}$,
两列相比得到:$si{n}^{2}\frac{1}{2}α$=sin(β-$\frac{1}{2}$α)•sin(γ-$\frac{1}{2}$α),
∴1-cosα=cos(β-γ)-cos(β+γ-α),1+cos(β+γ-α)=cos(β-γ)+cosα.
∵β+γ-α=180°-2α,
∴2sin2α=2sinβsinγ,
∴BC2=AC•AB.
点评 本题考查了三角形的内角和,正弦定理,三角函数,正确掌握正弦定理是解题的关键.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{42}}{6}$ | B. | $\frac{7}{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
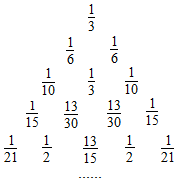
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{12}$ | D. | $\frac{11}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com