练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知下列随机变量：
    ①10件产品中有2件次品，从中任选3件，取到次品的件数X；
    ②一位射击手对目标进行射击，击中目标得1分，未击中目标得0分，用X表示该射击手在一次射击中的得分；
    ③刘翔在一次110米跨栏比赛中的成绩X；
    ④在体育彩票的抽奖中，一次摇号产生的号码数X．
    其中X是离散型随机变量的是（　　）
    A．①②③B．②③④C．①②④D．③④

    分析 利用离散型随机变量的定义求解．

    解答 解：①10件产品中有2件次品，从中任选3件，取到次品的件数X是一个可变化的整数，故是离散型随机变量，正确；
    ②一位射击手对目标进行射击，击中目标得1分，未击中目标得0分，用X表示该射击手在一次射击中的得分，是一个可变化的整数，故是离散型随机变量，正确；
    ③刘翔在一次110米跨栏比赛中的成绩X，是在范围内的，因此不是一个离散型的随机变量，不正确；
    ④在体育彩票的抽奖中，一次摇号产生的号码数X，是一个可变化的整数，故是离散型随机变量，正确．
    故选：C．

    点评 本题考查判断一组变量是否是离散型随机变量，是一个概念题，解题时注意理解离散型随机变量的概念，学会判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．sin65°cos20°-cos65°sin20°=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{\sqrt{2}}{2}$D．-$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

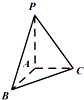
    8．如图，三菱锥P-ABC中，PA⊥平面ABC，∠BAC=90°，则二面角B-PA-C的大小等于（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中ω＞0．设f（x）=$\overrightarrow{OA}$•$\overrightarrow{OB}$．
    （1）记函数y=f（x）的正的零点从小到大构成数列{an}（n∈N*），当a=$\sqrt{3}$，b=1，ω=2时，求{an}的通项公式与前n项和Sn；
    （2）令ω=1，a=t2，b=（1-t）2，若不等式f（θ）-$\sqrt{ab}$＞0对任意的t∈[0，1]恒成立，求θ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=sin（2x+$\frac{π}{6}$）+2sin2x
    （1）求函数f（x）的最小正周期；
    （2）求函数f（x）的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某艺术学校要排一张有3个舞蹈节目和4个歌唱节目的演出节目单，要求：
    （1）任何两个舞蹈节目不相邻的排法有多少种？
    （2）歌唱节目与舞蹈节目间隔排列的方法有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某种产品的广告费支出x与销售额y（单位：万元）之间有如表对应数据：
    x24568
    y3040605070
    （1）求广告费支出x与销售额y回归直线方程$\hat y$=bx+a（a，b∈R）；
    已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
    （2）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．两平行直线3x-4y-3=0和6x-8y+5=0之间的距离是$\frac{11}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设A、B为两个独立事件，若P（A）=0.4，P（A∪B）=0.7．则P（B）=（　　）
    A．0.6B．0.5C．0.4D．0.3

    查看答案和解析>>

    同步练习册答案