
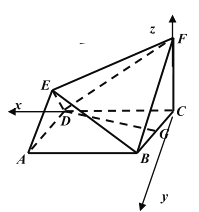
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,
,![]() .
.
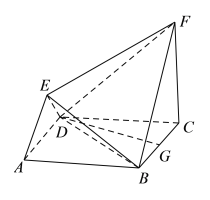
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)通过证明平面![]() 与平面
与平面![]() 都和直线
都和直线![]() 垂直可得;
垂直可得;
(2) 以![]() 为原点
为原点![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示的空间直角坐标系,写出各点坐标,求出二面角两个面的法向量,由法向量的夹角得二面角(要判断二面角的范围).
轴,建立如图所示的空间直角坐标系,写出各点坐标,求出二面角两个面的法向量,由法向量的夹角得二面角(要判断二面角的范围).
(1)证明:∵四边形![]() 是菱形,
是菱形,![]() ,
,![]() 是等边三角形,又
是等边三角形,又![]() 为
为![]() 的中点,∴
的中点,∴![]() ,而
,而![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() 面ADE.
面ADE.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)由(1)平面![]() 平面
平面![]() ,
,![]() ,则
,则![]() 到
到![]() 的距离为1,所以
的距离为1,所以![]() 到平面
到平面![]() 距离是1,以
距离是1,以![]() 为原点
为原点![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 与
与![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则![]() ,
,![]() ,所以
,所以![]() ,
,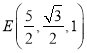 ,
,![]() ,
, 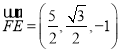 ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量是
的一个法向量是![]() ,
,
则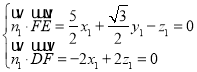 ,取
,取![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,
同理可得面![]() 的一个法向量
的一个法向量![]()
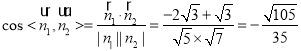 ,二面角
,二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图数据如图.根据茎叶图,下列描述正确的是( )
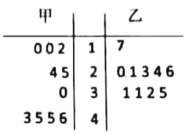
A.甲种树苗的中位数大于乙种树苗的中位数,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的中位数大于乙种树苗的中位数,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的中位数大于甲种树苗的中位数,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的中位数大于甲种树苗的中位数,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 是正方体,
是正方体,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面与棱
的平面与棱![]() 交于点
交于点![]() ,则以下说法不正确的是( )
,则以下说法不正确的是( )
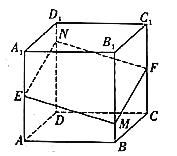
A.四边形![]() 是平行四边形
是平行四边形
B.四边形![]() 是菱形
是菱形
C.当点![]() 从点
从点![]() 往点
往点![]() 运动时,四边形
运动时,四边形![]() 的面积先增大后减小
的面积先增大后减小
D.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积一直增大
的体积一直增大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,且
,且![]() .过椭圆的右焦点
.过椭圆的右焦点![]() 作长轴的垂线与椭圆,在第一象限交于点
作长轴的垂线与椭圆,在第一象限交于点![]() ,且满足
,且满足![]() .
.
(1)求椭圆的标准方程;
(2)若矩形![]() 的四条边均与椭圆相切,求该矩形面积的取值范围.
的四条边均与椭圆相切,求该矩形面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.同比一般情况下是今年第n月与去年第n月比;环比,表示连续2个统计周期(比如连续两月)内的量的变化比.如图是根据国家统计局发布的2019年4月—2020年4月我国CPI涨跌幅数据绘制的折线图,根据该折线图,则下列说法正确的是( )
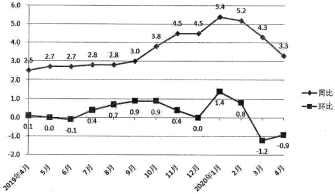
A.2020年1月CPI同比涨幅最大
B.2019年4月与同年12月相比较,4月CPI环比更大
C.2019年7月至12月,CPI一直增长
D.2020年1月至4月CPI只跌不涨
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com