练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知命题p：{x||x-1|＜c（c＞0）}，命题q：{x||x-3|＞4}，且￢p是q成立的充分且不必要条件，求实数c的取值范围．

    分析 根据绝对值不等式的解法，结合充分条件和必要条件的定义建立不等式关系进行求解即可．

    解答 解：由|x-1|＜c得1-c＜x＜1+c，即p：{x|1-c＜x＜1+c}，￢p：{x|x＞1+c或x＜1-c}，
    由|x-3|＞4，得x-3＞4或x-3＜-4，得x＞7或x＜-1，即q：{x|x＞7或x＜-1}，
    ∵￢p是q成立的充分且不必要条件，
    ∴$\left\{\begin{array}{l}{1+c≥7}\\{1-c≤-1}\\{c＞0}\end{array}\right.$得$\left\{\begin{array}{l}{c≥6}\\{c≥2}\\{c＞0}\end{array}\right.$得c≥6，
    即实数c的取值范围是[6，+∞）．

    点评 本题主要考查充分条件和必要条件的应用，根据条件建立不等式关系是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．根据下列条件，求双曲线方程：
    （1）中心在原点，一个顶点是（0，6），且离心率是1.5；
    （2）已知双曲线经过点P（10，-3$\sqrt{3}$），且渐近线为y=±$\frac{3}{5}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=x2-4x+3．
    （1）求f[f（-1）]的值；
    （2）求函数f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知cos（α+β）=$\frac{5}{13}$，cosβ=$\frac{4}{5}$，且α、β均为锐角，则cosα=$\frac{56}{65}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．比较大小：f（x）=xsinx+cosx，则f（$\frac{π}{12}$）＜f（$\frac{π}{8}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若实数x、y满足xy＞0，则$\frac{x}{x+y}$+$\frac{2y}{x+2y}$的最大值为（　　）
    A．2-$\sqrt{2}$B．2$+\sqrt{2}$C．4$-2\sqrt{2}$D．4$+2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．计算下列各式的值：
    （1）$\frac{lg12}{1+\frac{1}{2}lg0.36+\frac{1}{3}lg8}$；
    （2）（$\frac{25}{9}$）0.5+0.1-2+（$\sqrt{8}$）${\;}^{{\;}^{\frac{2}{3}}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知集合M={x|-$\sqrt{5}$＜x＜$\sqrt{3}$，x∈Z}，则下列集合是集合M的子集的为（　　）
    A．P={-3，0，1}B．Q={-1，0，1，2}C．R={y|-π＜y＜-1，y∈Z}D．S={x||x|≤$\sqrt{3}$，x∈N}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

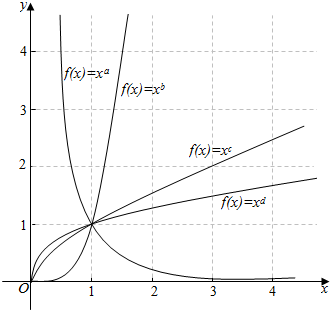
    16．如图示中的幂函数在第一象限的图象，则下面四个选项中正确的是（　　）
    A．a+b+c+d为正数B．b+c+d-a可能为零
    C．a-b-c-d为负数D．b×c×d×a符号不能确定

    查看答案和解析>>

    同步练习册答案