
���� �������������ʹ�ʽ��a��b��c�Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
������$\overrightarrow{F_1P}$=2$\overrightarrow{F_1Q}$��֪QΪF1P���е㣬����Q��0��y������F1��-1��0������P��1��2y����������Բ���̣����P�����꣬���ֱ��PF1�ķ��̣�������Բ���̣�����Τ�ﶨ�����ҳ���ʽ�����㼴�ɵõ�����ֵ��
��� �⣺��������֪������$\frac{c}{a}$=$\frac{1}{2}$��2c=2��
��c=1��a=2����b=$\sqrt{3}$��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
������$\overrightarrow{F_1P}$=2$\overrightarrow{F_1Q}$��֪QΪF1P���е㣬
����Q��0��y������F1��-1��0������P��1��2y����
��P������Բ�ķ��̣��������y=��$\frac{3}{4}$����ȡP��1��$\frac{3}{2}$����
�ɵ�ֱ��PF1�ķ���Ϊy=$\frac{3}{4}$��x+1����������Բ���̣�
�ɵ�7x2+6x-13=0��
��P��x1��y1����R��x2��y2����
��x1+x2=-$\frac{6}{7}$��x1x2=-$\frac{13}{7}$��
���ҳ���ʽ�ɵ�|PR|=$\sqrt{1+\frac{9}{16}}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$
=$\frac{5}{4}$•$\sqrt{\frac{36}{49}+\frac{52}{7}}$=$\frac{25}{7}$��
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ�������ҳ�����ע������ֱ�߷��̺���Բ���̣�����Τ�ﶨ�����ҳ���ʽ��ͬʱ�����������߶��������ã������е��⣮


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{3}}}{3}$ | B�� | $-\frac{{\sqrt{3}}}{3}$ | C�� | $-\frac{{\sqrt{6}}}{9}$ | D�� | $\frac{{5\sqrt{3}}}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{10}$ ��$\frac{{2\sqrt{2}}}{3}$ | B�� | $\sqrt{10}$ | C�� | $\frac{{2\sqrt{2}}}{3}$ | D�� | $\frac{1}{3}$��$\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��-\frac{1}{2}��+�ޣ�$ | B�� | $��-\frac{1}{2}��0���ȣ�0��+�ޣ�$ | C�� | $[-\frac{1}{2}��+�ޣ�$ | D�� | [0��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
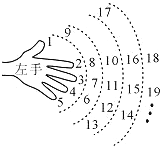 ��ͼ��һ��С���Ѱ���ͼ��ʾ�Ĺ�����ϰ������1��Ĵָ��2ʳָ��3��ָ��4����ָ��5Сָ��6����ָ������һֱ����2015ʱ����Ӧ��ָͷ����ָ����ָͷ�����ƣ���
��ͼ��һ��С���Ѱ���ͼ��ʾ�Ĺ�����ϰ������1��Ĵָ��2ʳָ��3��ָ��4����ָ��5Сָ��6����ָ������һֱ����2015ʱ����Ӧ��ָͷ����ָ����ָͷ�����ƣ����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com