考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(Ⅰ)连结AB1,交A1B于点O,连结OD,利用三角形的中位线定理,推导出OD∥B1C,由此能够证明B1C∥平面A1BD.
(Ⅱ)以D为坐标原点,以DC为x轴,以DB为y轴,以过D点垂直于AC的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角A1-BD-B1的余弦值.
解答:
解:(Ⅰ)连结AB
1,交A
1B于点O,连结OD,

∵在直三棱柱ABC-A
1B
1C
1中,AA
1=AB=BC=3,
∴ABB
1A
1是正方形,∴O是AB
1的中点,
∵D是AC的中点,∴OD是△ACB
1的中位线,∴OD∥B
1C,
∵B
1C不包含于平面A
1BD,OD?平面A
1BD,
∴B
1C∥平面A
1BD.
(Ⅱ)以D为坐标原点,以DC为x轴,以DB为y轴,
以过D点垂直于AC的直线为z轴,建立空间直角坐标系,
∵AA
1=AB=BC=3,AC=2,D是AC的中点,
∴A
1(-1,0,3),B(0,2
,0),
D(0,0,0),B
1(0,2
,3),
∴
=(-1,0,3),
=(0,2
,0),
=(0,2
,3),
设平面A
1BD的法向量
=(x,y,z),则
•=0,
•=0,
∴
,∴
=(3,0,1),
设平面B
1BD的法向量
=(x
1,y
1,z
1),则
•=0,
•=0,
∴
,∴
=(1,0,0),
设二面角A
1-BD-B
1的平面角为θ,
cosθ=|cos<
,>|=|
|=
.
∴二面角A
1-BD-B
1的余弦值为
.
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要注意向量法的合理运用.

 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC=3,AC=2,D是AC的中点.


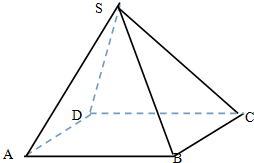 如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.
如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米. 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=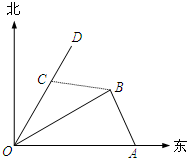 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.