考点:利用导数研究曲线上某点切线方程,函数零点的判定定理
专题:计算题,分类讨论,导数的概念及应用,导数的综合应用
分析:(1)求出导数,求出切线的斜率和切点,再由斜截式方程,即可得到切线方程;
(2)求出g(x)的导数,对a讨论,a≤0,a>0,结合函数的单调性,即可求得a的范围;
(3)构造h(x)=f(x)-g(x)=(x-2)e
x-ax
3+x+2,转化h(x)=(x-2)e
x-ax
3+x+2≥0在[0,+∞)上恒成立,通过h'(0)=0,对a
≤时,a
>时,判断函数的单调性,以及函数的最值,是否满足题意,求出k的最大值.
解答:
解:(1)f′(x)=e
x+(x-2)e
x=(x-1)e
x,
则f(x)在点(0,f(0))处的切线斜率为(0-1)e
0=-1,
切点为(0,-2),则切线方程为y=-x-2;
(2)g(x)=ax
3-3x
2+1,g′(x)=3ax
2-6x,
当a≤0时,g(x)在x>0,g′(x)<0,则g(x)递减,则g(x)在x∈(0,+∞)内只有一个零点;
当a>0时,g′(x)>0,解得,x>
,g′(x)<0,解得0<x<
,
则g(
)取极小值,由于g(0)=1,则只要g(
)=0,即有g(x)在x∈(0,+∞)内只有一个零点.
由g(
)=a
•-
+1=0,解得a=2(-2舍去).
则a的取值范围是(-∞,0]∪{2};
(3)令h(x)=f(x)-g(x)=(x-2)e
x-ax
3+x+2,
依题可知h(x)=(x-2)e
x-ax
3+x+2≥0在[0,+∞)上恒成立,
h'(x)=(x-1)e
x-3ax
2+1,令φ(x)=h'(x)=(x-1)e
x-3ax
2+1,
有φ(0)=h'(0)=0且φ'(x)=x(e
x-6a),
①当6a≤1,即a
≤时,
因为x≥0,e
x≥1,所以φ'(x)=x(e
x-6a)≥0
所以函数φ(x)即h'(x)在[0,+∞)上单调递增,又由φ(0)=h'(0)=0
故当x∈[0,+∞)时,h'(x)≥h'(0)=0,所以h(x)在[0,+∞)上单调递增,
又因为h(0)=0,所以h(x)≥0在[0,+∞)上恒成立,满足题意;
②当6a>1,即a>
时,
当x∈(0,ln(6a)),φ'(x)=x(e
x-6a)<0,函数φ(x)即h'(x)单调递减,
又由φ(0)=h'(0)=0,所以当x∈(0,ln(6a)),h'(x)<h'(0)=0
所以h(x)在(0,ln(6a))上单调递减,
又因为h(0)=0,所以x∈(0,ln(6a))时h(x)<0,
这与题意h(x)≥0在[0,+∞)上恒成立相矛盾,故舍.
综上a
≤,即a的最大值是
.
点评:本题考查导数的运用:求切线方程,求单调区间和极值、最值,考查分类讨论的思想方法,考查运算能力,属于中档题.



 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案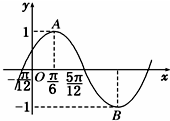 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<