
���� ����7��С����ȡ3��ȡ��Ϊ${C}_{7}^{3}$����ȡһ��������˵����һ��ȡ��һ��2�ף��������֪ʶ����ȡ���������Ȼ�����ŵ���ʼ��㹫ʽ����
�������ж��������X�����п���ȡֵΪ200��50��10��0�������������������ĸ���ȡֵ�ĸ��ʣ��������ֲ��м�����ֵ��
��� �⣺��Ai��ʾ����i������Bj��ʾ����j��������Ai��i=0��1��2��3����Bj��j=0��1���������
����ǡ������1������ĸ���ΪP��A1��=$\frac{{C}_{3}^{1}{C}_{4}^{2}}{{C}_{7}^{3}}=\frac{18}{35}$=�� ����4�֣�
����X�����п���ֵΪ��0��10��50��200��
P��X=200��=P��A3B1��=P��A3��P��B1��=$\frac{{C}_{3}^{3}}{{C}_{7}^{3}}��\frac{1}{3}=\frac{1}{105}$��
P��X=50��=P��A3B0��=P��A3��P��B0��=$\frac{{C}_{3}^{3}}{{C}_{7}^{3}}��\frac{2}{3}=\frac{2}{105}$��
P��X=10��=P��A2B1��=P��A2��P��B1��=$\frac{{C}_{3}^{2}{C}_{4}^{1}}{{C}_{7}^{3}}��\frac{1}{3}=\frac{4}{35}$��
P��X=0��=1-$\frac{1}{105}-\frac{2}{105}-\frac{4}{35}=\frac{6}{7}$�� ����11�֣�
����X�ķֲ���Ϊ
| X | 0 | 10 | 50 | 200 |
| P | $\frac{6}{7}$ | $\frac{4}{35}$ | $\frac{2}{105}$ | $\frac{1}{105}$ |
���� ������Ҫ�����˹ŵ���ͼ����㹫ʽ�������¼�����ɢ����������ķֲ��м�����ֵ����⣬���������ø���֪ʶ���ʵ�������������


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{2}}{2}$ | B�� | -$\frac{\sqrt{2}}{2}$ | C�� | $��\frac{\sqrt{2}}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$��1-2-9�� | B�� | $\frac{1}{3}$��1-2-9�� | C�� | -$\frac{4}{3}$��1+2-9�� | D�� | ��1-2-9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
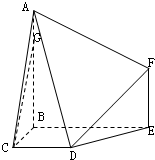 ��ͼ���ڶ�����ABCDEF�У�BA��BE��BA��BC��BE��BC��AB��EF��CD��BE��AB=BE=2��BC=CD=EF=1��G���߶�AB�ϣ���BG=3GA��
��ͼ���ڶ�����ABCDEF�У�BA��BE��BA��BC��BE��BC��AB��EF��CD��BE��AB=BE=2��BC=CD=EF=1��G���߶�AB�ϣ���BG=3GA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͼ����ڵ�$��{-\frac{��}{3}��0}��$���ĶԳ� | B�� | ͼ�����$x=-\frac{��}{6}$��Գ� | ||
| C�� | ������$[{-\frac{5��}{12}��-\frac{��}{6}}]$�ϵ������� | D�� | ������$[{-\frac{��}{6}��\frac{��}{3}}]$�ϵ����ݼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com