
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
【答案】
(1)解:由方程x2+y2+2x+4y+3=0知(x+1)2+(y-2)2=2,所以圆心为(-1,2),半径为 ![]() .
.
当切线过原点时,设切线方程为y=kx,则 ![]() =
= ![]() ,所以k=2±
,所以k=2± ![]() ,即切线方程为y=(2±
,即切线方程为y=(2± ![]() )x.
)x.
当切线不过原点时,设切线方程为x+y=a,则 ![]() =
= ![]() ,所以a=1或a=3,即切线方程为x+y+1=0或x+y3=0.
,所以a=1或a=3,即切线方程为x+y+1=0或x+y3=0.
综上知,切线方程为y=(2± ![]() )x或x+y+1=0或x+y-3=0;
)x或x+y+1=0或x+y-3=0;
(2)因为|PO|2+r2=|PC|2,所以x12+y12+2=(x1+1)2+(y1-2)2,即2x1-4y1+3=0.
要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x-4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,
此时P点即为两直线的交点,得P点坐标(- ![]() ,
, ![]() ).
).
【解析】(1)将圆的一般方程变为标准方程,得到圆心坐标和半径,分切线过原点和不过原点设方程,由点到直线的距离等于半径列出等式,得到切线方程;(2)在直角△PMC中,根据勾股定理得出![]() ,列出等式得到P点的轨迹方程,当直线PO垂直于直线2x-4y+3=0时,|PM|最小,联立解出交点坐标.
,列出等式得到P点的轨迹方程,当直线PO垂直于直线2x-4y+3=0时,|PM|最小,联立解出交点坐标.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: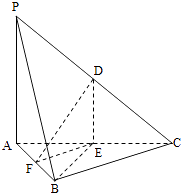
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个容量为M的样本数据,其频率分布表如下.
(1)计算a,b的值;
(2)画出频率分布直方图;
(3)用频率分布直方图,求出总体的众数及平均数的估计值.
频率分布表
分组 | 频数 | 频率 | 频率/组距 |
(10,20] | 2 | 0.10 | 0.010 |
(20,30] | 3 | 0.15 | 0.015 |
(30,40] | 4 | 0.20 | 0.020 |
(40,50] | a | b | 0.025 |
(50,60] | 4 | 0.20 | 0.020 |
(60, 70] | 2 | 0.10 | 0.010 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图所示:将
的一段图象如图所示:将![]() 的图象向右平移
的图象向右平移![]() (
(![]() )个单位,可得到函数
)个单位,可得到函数![]() 的图象,且图象关于原点对称.(1)求
的图象,且图象关于原点对称.(1)求![]() 的值.
的值.
(2)求![]() 的最小值,并写出
的最小值,并写出![]() 的表达式.
的表达式.
(3)设t>0,关于x的函数![]() 在区间
在区间![]() 上最小值为-2,求t的范围.
上最小值为-2,求t的范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
(1)若∠POB=θ,试将四边形OPDC的面积y表示为关于θ的函数;
(2)求四边形OPDC面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com