练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．用数学归纳法证明n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2，（n∈N*）时，若记f（n）=n+（n+1）+（n+2）+…+（3n-2），则f（k+1）-f（k）等于（　　）
    A．3k-1B．3k+1C．8kD．9k

    分析 数学归纳法证明n=k+1的待证表达式，可以利用n=k时的表达式写出即可．

    解答 解：因为f（k）=k+（k+1）+（k+2）+…+（3k-2），
    f（k+1）=（k+1）+（k+2）+…+（3k-2）+（3k-1）+（3k）+（3k+1）
    则f（k+1）-f（k）=3k-1+3k+3k+1-k=8k
    故选：C

    点评 本题考查数学归纳法的应用，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知函数$f（x）=sin（2x+\frac{π}{6}）+sin（2x-\frac{π}{6}）+cos2x+1$
    （1）求函数f（x）的对称中心和函数的单调递增区间；
    （2）已知△ABC中，角A，B，C的对边分别为a，b，c，若$f（A）=3，B=\frac{π}{4}，a=\sqrt{3}$，求AB．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知{an}为等差数列，Sn为数列{an}的前n项和，平面内三个不共线向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，满足$\overrightarrow{OC}=（{{a_{17}}-3}）\overrightarrow{OA}+{a_{2001}}\overrightarrow{OB}$，若点A，B，C在一条直线上，则S2017=（　　）
    A．2017B．4034C．2016D．4032

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设随机变量X～N（μ，σ2），且$P（X＜1）=\frac{1}{2}$，$P（X＞2）=\frac{1}{5}$，则P（0＜X＜1）=0.3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．给出一个命题P：若a，b，c，d∈R，a+b=1，c+d=1，且ac+bd＞1，则a，b，c，d中至少有一个小于零．在用反证法证明P时，应该假设（　　）
    A．a，b，c，d中至少有一个正数B．a，b，c，d全为正数
    C．a，b，c，d全都大于或等于0D．a，b，c，d中至多有一个负数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．若由曲线y=x2+k2与直线y=2kx（k＞0）及y轴所围成的平面图形的面积S=9，则k=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．下列表示旅客搭乘动车的流程中，正确的是（　　）
    A．买票→候车厅候车→上车→候车检票口检票
    B．候车厅候车→买票→上车→候车检票口检票
    C．买票→候车厅候车→候车检票口检票→上车
    D．候车厅候车→上车→候车检票口检票→买票

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

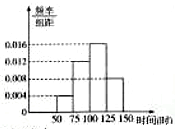    2．某公司为了解该公司800名员工参加运动的情况，对公司员工半年来的运动时间进行统计得到如图所示的频率分布直方图，则运动时间超过100小时的员工有（　　）
    A．360人B．480人C．600人D．240人

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=lnx-ax，$g（x）=\frac{1}{x}+a$．
    （1）讨论函数F（x）=f（x）-g（x）的单调性；
    （2）若f（x）•g（x）≤0在定义域内恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案