练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下面几种推理是合情推理的是(　　)

    ①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形内角和是 归纳出所有三角形的内角和都是;③由,满足,,推出是奇函数;④三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是.

    A. ①②B. ①③④C. ①②④D. ②④

    【答案】C

    【解析】

    由题意可知：①是类比推理，②是归纳推理，③是演绎推理，④是归纳推理，据此确定所给的命题是否属于合情推理即可.

    逐一考查所给的推理：

    ①由圆的性质类比出球的有关性质是类比推理，属于合情推理;

    ②由直角三角形、等腰三角形、等边三角形内角和是 归纳出所有三角形的内角和都是是归纳推理，属于合情推理;

    ③由,满足,,推出是奇函数是演绎推理，不属于合情推理;

    ④三角形内角和是,四边形内角和是,五边形内角和是,由此得凸多边形内角和是是归纳推理，属于合情推理.

    综上可得：合情推理的编号为①②④.

    本题选择C选项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

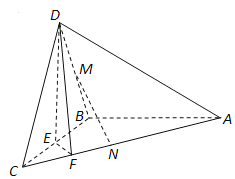
    【题目】如图,在三棱锥中,已知是正三角形, 平面为的中点, 在棱上,且.

    (1)求三棱锥的体积;

    (2)求证: 平面;

    (3)若为中点, 在棱上,且,求证: 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

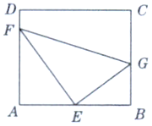
    【题目】如图，某污水处理厂要在个矩形ABCD的池底水平铺设污水净化管道（，E是直角顶点）来处理污水，管道越长，污水净化效果越好，设计要求管道的接口E是AB的中点，F、G分别落在AD、BC上，且，，设.

    （1）试将污水管道的长度l表示成的函数，并写出定义域；

    （2）当为何值时，污水净化效果最好，并求此时管道的长度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A（–1，2），B（2，8）以及，=–13，求点C、D的坐标和的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象的一个对称中心与它相邻的一条对称轴之间的距离为．

    （1）求函数f（x）的对称轴方程及单调递增区间；

    （2）将函数y=f（x）的图象向右平移个单位后，再将得到的图象上所有点的横坐标缩短到原来的（纵坐标不变），得到函数y=g（x）的图象，当x∈（，）时，求函数g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆和椭圆， 是椭圆的左焦点．

    （Ⅰ）求椭圆的离心率和点的坐标；

    （Ⅱ）点在椭圆上，过作轴的垂线，交圆于点（不重合），是过点的圆的切线．圆的圆心为点，半径长为．试判断直线与圆的位置关系，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.

    (1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果,且,,那么;

    (2)请你运用上述对数运算性质计算的值;

    (3)因为,所以的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断的位数.(注)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行六面体中，．

    求证：（1）；

    （2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象所过的定点为，光线沿直线射入，遇直线后反射，且反射光线所在的直线经过点，求的值和的方程．

    查看答案和解析>>

    同步练习册答案