Question

已知函数f（x）=

2 sinx

1+cos2x-sin2x

．
（1）求函数的定义域；
（2）用定义判断f（x）的奇偶性；
（3）在[-π，π]上作出f（x）的图象；
（4）写出f（x）的最小正周期及单调区间．

Answer 1

考点：三角函数中的恒等变换应用,函数的定义域及其求法,函数奇偶性的判断

专题：三角函数的求值,三角函数的图像与性质

分析：（1）首先对函数的解析式进行化简，把函数的关系式化简成最简形式，进一步求出函数的定义域．
（2）首先判断函数的定义域关于原点对称，进一步利用f（-x）=-f（x）得到函数为奇函数．
（3）根据（2）的结论直接利用对称性，画出函数的图象．
（4）利用函数的解析式直接求出函数的最小正周期和单调区间．

解答： 解：函数f（x）=

2 sinx

1+cos2x-sin2x

=

2 sinx

1+cos2x

=

2 sinx

2 |cosx|

=

sinx

|cosx|

（1）要使函数有意义只需满足cosx≠0即可．
则：x≠kπ+

π

2

（k∈Z）
所以函数的定义域为：{x|x≠kπ+

π

2

}（k∈Z）
（2）由于：{x|x≠kπ+

π

2

}（k∈Z）的区间关于原点对称，
且满足f（-x）=

sin(-x)

|cos(-x)|

=-

sinx

|cosx|

=-f(x)
所以函数f（x）为奇函数．
（3）f（x）=

sinx

|cosx|

=±tanx
直接利用函数的对称性（关于原点对称）画出图形．
所以：函数f（x）=tanx的图象为：


所以：函数f（x）=-tanx的图象为：

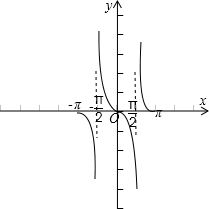
（4）根据函数的解析式：f（x）=±tanx
所以函数的最小正周期为：T=

π

1

=π
函数的单调区间为：
①当f（x）=tanx时，函数的单调递增区间为：(kπ-

π

2

，kπ+

π

2

)（k∈Z）
②当f（x）=-tanx时，函数的单调递减区间为：(kπ-

π

2

，kπ+

π

2

)（k∈Z）

点评：本题考查的知识要点：三角函数关系式的恒等变换，函数的定义域的应用，函数的周期的应用，函数的单调性的应用，利用函数的对称性确定函数的图象．