考点:余弦函数的图象,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)作出函数f(x)=
的图象,如图所示:
(2)由f(x)=
,分当-π<x<0时,和当0≤x≤π时两种情况,分别求得x的值,综上可得结论.
(3)若a∈R,讨论方程f(x)=a的解的个数,即函数f(x)的图象和直线y=a的交点个数.数形结合可得结论
解答:

解:(1)作出函数f(x)=
的图象,如图所示:
(2)∵f(x)=
,当-π<x<0时,由cosx=
,可得x=-
.
当0≤x≤π时,由sinx=
,可得x=
,或x=
.
综上可得,要求的x的值共计三个:x=-
,或x=
,或x=
.
(3)若a∈R,讨论方程f(x)=a的解的个数,
即函数f(x)的图象和直线y=a的交点个数.
数形结合可得,
当a>1,或 a<-1时,函数f(x)的图象和直线y=a
的交点个数为0;
当-1≤a<0时,函数f(x)的图象和直线y=a的交点个数为1;
当a=1时,函数f(x)的图象和直线y=a的交点个数为2;
当0≤a<1时,函数f(x)的图象和直线y=a的交点个数为3.
点评:本题主要考查正弦函数、余弦函数的图象,解三角方程,方程的根的存在性及个数判断,体现了数形结合、分类讨论、转化的数学思想,属于基础题.

 解:(1)作出函数f(x)=
解:(1)作出函数f(x)=

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案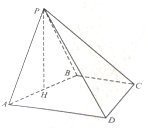 如图,四棱锥P-ABCD,底面ABCD为直角梯形,BC∥AD,BC⊥CD,BC=CD=
如图,四棱锥P-ABCD,底面ABCD为直角梯形,BC∥AD,BC⊥CD,BC=CD=