
| A. | 18π | B. | 20π | C. | 24π | D. | 20$\sqrt{3}$π |
分析 由三棱锥P-ABC的体积为2$\sqrt{3}$,求出PA,将三棱锥补成三棱柱,可得球心在三棱柱的中心,球心到底面的距离d等于三棱柱的高PA的一半,求出球的半径,然后求出球的表面积.
解答 解:∵三棱锥P-ABC的体积为2$\sqrt{3}$,
∴$\frac{1}{3}×\frac{\sqrt{3}}{4}×(2\sqrt{3})^{2}×PA$=2$\sqrt{3}$,
∴PA=2,
将三棱锥补成三棱柱,可得球心在三棱柱的中心,球心到底面的距离d等于三棱柱的高PA的一半,
∵△ABC是边长为2$\sqrt{3}$的正三角形,
∴△ABC外接圆的半径r=2,
∴球的半径为$\sqrt{5}$,
∴球O的表面积为4π•5=20π.
故选:B.
点评 本题考查球的内接体与球的关系,考查空间想象能力,利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键.


科目:高中数学 来源: 题型:解答题
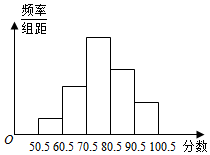 从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:
从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a⊥α,b⊥α,则a⊥b | B. | a∥α,b?α,则a∥b | C. | a⊥b,b?α,则a⊥α | D. | a∥α,b?α,则a∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
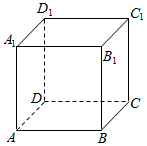 在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小
在正方体ABCD-A1B1C1D1中,求下列异面直线所成角的大小查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com