
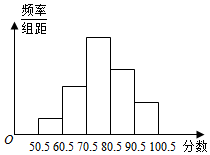
 从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:
从全校参加信息技术知识竞赛学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比是1:3:6:4:2,最中间一组的频数是18,请结合直方图提供的信息,解答下列问题:分析 (1)根据最右边一组的频数是6,而频率等于该组的面积在整个图形面积中的百分比,因此可得样本容量为48;
(2)根据分层抽样,即可求出各小组的人数.
解答 解:在频率分布直方图中,长方形的高之比=面积之比=频数之比=频率之比
(1)∵最右边一组的频数是6,从左到右各小组的长方形的高之比为1:3:6:4:2
∴设样本容量为n,得(1+3+6+4+2):n=2:6
∴n=48,样本容量为48,
(2)第3组抽取的人数为6×$\frac{6}{6+4+2}$=2,
第4组抽取的人数为6×$\frac{4}{6+4+2}$=3,
第5组抽取的人数为6×$\frac{2}{6+4+2}$=1,
点评 本题考查了频率直方图的有关知识以及分层抽样,属于基础题.频率直方图中,各个小长方形的面积等于该组数据的频率,所有长方形的面积之和等于1.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x>1或-1<x<0} | B. | {x|x>1或x<-1} | C. | {x|0<x<1或x<-1} | D. | {x|-1<x<1且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab有最大值$\frac{1}{4}$ | B. | $\frac{1}{a}$+$\frac{1}{b}$有最小值5 | ||
| C. | $\sqrt{a}$+$\sqrt{2b}$有最大值1+$\sqrt{2}$ | D. | a2+4b2有最小值$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18π | B. | 20π | C. | 24π | D. | 20$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com