
分析 (1)判断直线与椭圆的位置关系,求出切点坐标,利用$\overrightarrow{AM}=λ\overrightarrow{AB}$.化简求解即可.
(2)利用(1)以及△MF1F2的周长为6,求出椭圆的几何量,然后求解椭圆方程.
解答 解:(1)证明:椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,({a>b>0})$,
直线l:y=ex+a,消去y并化简可得x2+2cx+c2=0,
可得x=-c,△=0,可知直线与椭圆相切,
切点坐标(-c,$\frac{{b}^{2}}{a}$),A(-$\frac{{a}^{2}}{c}$,0),B(0,a),
由$\overrightarrow{AM}=λ\overrightarrow{AB}$.可得:
λ=$\frac{{a}^{2}-{c}^{2}}{{a}^{2}}$=1-e2.
(2)由$\left\{\begin{array}{l}{1-{e}^{2}=\frac{3}{4}}\\{2a+2c=6}\end{array}\right.$,解得a=2,c=1,可得b2=3,
所以所求椭圆方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
点评 本题考查直线与椭圆的位置关系的应用,考查转化思想以及计算能力.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 1.5 | 1.75 | 1.625 | 1.6875 |
| f(x) | -5.00 | 4.00 | -1.63 | 0.86 | -0.46 | 0.18 |
| A. | 1.50 | B. | 1.66 | C. | 1.70 | D. | 1.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
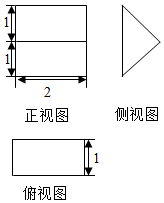 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com