
| A. | (0,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (0,+∞) |
分析 设t=sinx,由x∈(0,π)和正弦函数的性质求出t的范围,将t代入f(x)后求出函数的导数,求出临界点,根据条件判断出函数的单调性,由导数与函数单调性的关系列出不等式,求出实数a的取值范围.
解答 解:设t=sinx,由x∈(0,π)得t∈(0,1],
∵f(x)=sin3x+acos2x=sin3x+a(1-sin2x),
∴f(x)变为:y=t3-at2+a,
则y′=3t2-2at=t(3t-2a),
由y′=0得,t=0或t=$\frac{2a}{3}$,
∵f(x)=sin3x+acos2x在(0,π)上存在最小值,
∴函数y=t3-at2+a在(0,1]上递减或先减后增,
即$\frac{2a}{3}$>0,得a>0,
∴实数a的取值范围是(0,+∞),
故选:D.
点评 本题考查正弦函数的性质,导数与函数单调性的关系,以及构造法、换元法的应用,考查化简、变形能力.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{5π}{6}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{5π}{6}$] | C. | [$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [0,$\frac{π}{6}$]∪[$\frac{5π}{6}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{3}{4}x$ | B. | $y=±\frac{4}{3}x$ | C. | $y=±\frac{16}{9}x$ | D. | $y=±\frac{9}{16}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
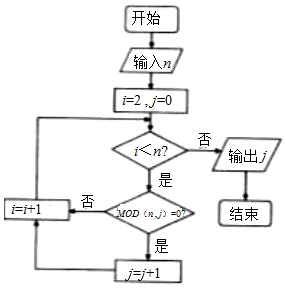
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com