考点:复合函数的单调性,对数函数的图像与性质
专题:函数的性质及应用
分析:(1)把A(2,1)、B(5,2)两点坐标代入f(x)的解析式,可得a、b的值,从而求得f(x)的解析式.
(2)设t=log
3x,F(x)可转化为y=t
2-t-2=
(t-)2-
(-2≤t≤2),再利用二次函数的性质求得函数的最大值及其相对应的x值.
解答:
解:(1)把图象中A(2,1)、B(5,2)两点坐标代入f(x)=log
3(ax+b),
化简可得2a+b=3 且5a+b=9,解得a=2,b=-1,
故f(x)=log3(2x-1),令2x-1>0,求得函数的定义域为(
,+∞).
(2)F(x)=log
3(
)•log
3(3x)=(log
3x-2)•(log
3x+1),
设t=log
3x,x∈[
,9],则-2≤t≤2,∴F(x)可转化为y=t
2-t-2=
(t-)2-
(-2≤t≤2),
∴当t=
时,y
min=-
,此时x=3;当t=-2时,y
max=4,此时x=
.
综上知,当x=
时,最大值为F(
)=4.
点评:本题主要考查用待定系数法求函数的解析式,对数的运算性质、复合函数的单调性,二次函数的性质的用用,体现了转化的数学思想,属于中档题.

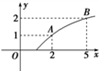 已知函数f(x)=log3(ax+b)的部分图象如图所示.
已知函数f(x)=log3(ax+b)的部分图象如图所示.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案