
分析 方法一,设直线l的方程为3x+4y+m=0,分别令x=0,y=0 求出直线在坐标轴上的截距即可得出;
方法二:设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1,利用相互平行的直线的充要条件即可得出.
解答 解:方法一,设直线l的方程为3x+4y+m=0----(3分)
令x=0得y轴上的截距b=$-\frac{m}{4}$----(5分)
令y=0得x轴上的截距a=$-\frac{m}{3}$----(7分)
所以$-\frac{m}{3}$+($-\frac{m}{4}$)=$\frac{7}{3}$----(9分)
解得m=-4--------------(11分)
所以所求直线方程为3x+4y-4=0------(12分)
方法二:设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1------(3分)
所以 a+b=$\frac{7}{3}$----(5分)
$-\frac{b}{a}=-\frac{3}{4}$----(8分)
解得a=$\frac{4}{3}$b=1--------(10分)
所以所求直线方程为$\frac{x}{{\frac{4}{3}}}+\frac{y}{1}=1$,------(11分)
即3x+4y-4=0--------(12分)
点评 本题考查了直线的截距式、相互平行的直线的充要条件,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={(\sqrt{x+1})^2}$ | B. | $y=\root{3}{x^3}+1$ | C. | $y=\frac{x^2}{x}+1$ | D. | $y=\sqrt{x^2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
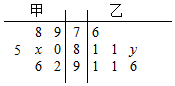 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 外心 | B. | 内心 | C. | 重心 | D. | 垂心 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com