
已知关于 的函数
的函数 ,其导函数为
,其导函数为 .记函数
.记函数 在区间
在区间 上的最大值为
上的最大值为 .
.
(1) 如果函数 在
在 处有极值
处有极值 ,试确定
,试确定 的值;
的值;
(2) 若 ,证明对任意的
,证明对任意的 ,都有
,都有 ;
;
(3) 若 对任意的
对任意的 恒成立,试求
恒成立,试求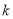 的最大值.
的最大值.
(1)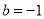 ,
, ;(2)证明详见解析;(3)
;(2)证明详见解析;(3)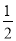 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数求函数的极值和最值等基础知识,考查学生的转化能力、分析问题解决问题的能力、计算能力.第一问,先对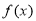 求导,由于
求导,由于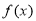 在x=1处有极值
在x=1处有极值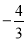 ,则
,则 ,
, ,列出方程组,解出b和c的值,由于得到了两组值,则需要验证看是否符合已知条件,若不符合需舍掉;第二问,可以利用二次函数图象和性质直接证明
,列出方程组,解出b和c的值,由于得到了两组值,则需要验证看是否符合已知条件,若不符合需舍掉;第二问,可以利用二次函数图象和性质直接证明 ,也可以利用反证法证明出矛盾,从而得到正确结论;第三问,结合第二问的结论,可以直接得到
,也可以利用反证法证明出矛盾,从而得到正确结论;第三问,结合第二问的结论,可以直接得到 时的情况,当
时的情况,当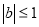 时需分
时需分 ,
, ,
,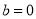 三种情况讨论,最后综合所有情况再得出结论.
三种情况讨论,最后综合所有情况再得出结论.
试题解析:(1) ∵ ,由
,由 在
在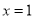 处有极值
处有极值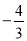 ,可得
,可得
 ,解得,
,解得, 或
或 2分
2分
若 ,
,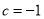 ,则
,则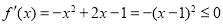 ,此时函数
,此时函数 没有极值; 3分
没有极值; 3分
若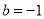 ,
, ,则
,则 ,此时当
,此时当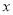 变化时,
变化时, ,
,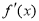 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴ 当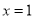 时,
时, 有极大值
有极大值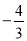 ,故
,故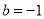 ,
, 即为所求。 4分
即为所求。 4分
(2)证法一:
当 时,函数
时,函数 的对称轴
的对称轴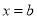 位于区间
位于区间 之外
之外
∴ 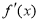 在区间
在区间 上的最值在两端点处取得,故
上的最值在两端点处取得,故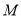 应是
应是 和
和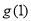 中较大的一个
中较大的一个
∴ 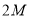

 ,即
,即 8分
8分
证法二(反证法):因为 ,所以函数
,所以函数 的对称轴
的对称轴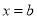 位于区间
位于区间 之外,
之外,
∴  在区间
在区间 上的最值在两端点处取得,故
上的最值在两端点处取得,故 应是
应是 和
和 中较大的一个,
中较大的一个,
假设 ,则
,则 ,将上述两式相加得: 6分
,将上述两式相加得: 6分
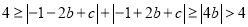 ,得
,得 ,产生矛盾,
,产生矛盾,
∴  8分
8分
(3) 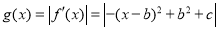
(ⅰ)当 时,由(2)可知
时,由(2)可知 ; 9分
; 9分
(ⅱ)当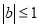 时,函数
时,函数 的对称轴
的对称轴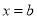 位于区间
位于区间 之内,
之内,
此时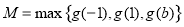 ,由
,由 ,有
,有
①若 ,则
,则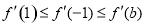 ,则
,则 ,
,
于是
 11分
11分
②若 ,则
,则 ,则
,则
于是
 13分
13分
综上可知,对任意的 、
、 都有
都有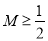
而当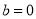 ,
,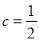 时,
时,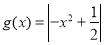 在区间
在区间 上的最大值
上的最大值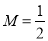 ,故
,故 对任意的
对任意的 、
、 恒成立的
恒成立的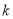 的最大值为
的最大值为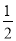 。 14分
。 14分
考点:导数的运算、利用导数求函数的极值和最值.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:2015届广东省高二下学期期中理科数学试卷(解析版) 题型:选择题
如图,四棱锥P-ABCD的底面为正方形,侧面PAD为等边三角形,且侧面PAD⊥底面ABCD.点M在底面内运动,且满足MP=MC,则点M在正方形ABCD内的轨迹



A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com