Question

3．△A BC是边长为2的等边三角形，已知向量$\vec a$，$\vec b$满足$\overrightarrow{{A}{B}}=2\vec a$，$\overrightarrow{{A}C}=2\vec a+\vec b$，则下列结论不正确的是（　　）

• A． $|{\overrightarrow b}|=2$
• B． $\overrightarrow a•\overrightarrow b=-1$
• C． $|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$
• D． $（{4\overrightarrow a+\overrightarrow b}）⊥\overrightarrow b$

Answer 1

分析 作出向量示意图，用三角形ABC的边表示出$\overrightarrow{a}$，$\overrightarrow{b}$，根据等比三角形的性质判断．

解答 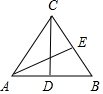解：取AB的中点D，BC的中点E，
∵$\overrightarrow{{A}{B}}=2\vec a$，$\overrightarrow{{A}C}=2\vec a+\vec b$，
∴$\overrightarrow{a}$=$\frac{1}{2}$$\overrightarrow{AB}$=$\overrightarrow{DB}$，$\overrightarrow{b}$=$\overrightarrow{AC}-2\overrightarrow{a}$=$\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}$，
∴|$\overrightarrow{b}$|=BC=2，故A正确；
$\overrightarrow{a}•\overrightarrow{b}$=$\overrightarrow{DB}•\overrightarrow{BC}$=1×2×cos120°=-1，故B正确；
|$\overrightarrow{a}+\overrightarrow{b}$|=|$\overrightarrow{DB}+\overrightarrow{BC}$|=|$\overrightarrow{DC}$|=CD=$\sqrt{3}$，故C错误；
$\overrightarrow{AE}$=2$\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$，
∵$\overrightarrow{AE}⊥\overrightarrow{BC}$，∴（2$\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$）⊥$\overrightarrow{b}$，∴（4$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{b}$，故D正确．
故选C．

点评 本题考查了平面向量的线性运算，属于基础题．