
分析 (1)求出f(x)的导数,由题意可得f(1)=0,f′(1)=2,解方程可得a,b的值;
(2)求得f(x),g(x)的解析式,求出导数,求得单调区间和极值、最值,即可得证.
解答 解:(1)f(x)=x+ax2+blnx的导数$f'(x)=1+2a+\frac{b}{x}(x>0)$,
由题意可得f(1)=1+a=0,f′(1)=1+2a+b=2,
得$\left\{{\begin{array}{l}{a=-1}\\{b=3}\end{array}}\right.$;
(2)证明:f(x)=x-x2+3lnx,g(x)=f(x)-2x+2=3lnx-x2-x+2(x>0),${g^′}(x)=\frac{3}{x}-2x-1=-\frac{(2x+3)(x-1)}{x}$,
| x | (0,1) | 1 | (1,+∞) |
| g′(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查运算能力,属于基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果两个复数的积是实数,那么这两个复数互为共轭复数 | |
| B. | 用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是:方程x2+ax+b=0至多有一个实根 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 在复平面中复数z满足|z|=2的点的轨迹是以原点为圆心,以2为半径的圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-x-2≤0 | B. | ?x∈R,x2-x-2<0 | C. | ?x∈R,x2-x-2≤0 | D. | ?x∈R,x2-x-2<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
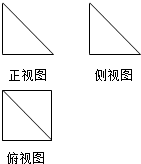 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com