
【题目】若存在常数![]() ,使得数列
,使得数列![]() 满足
满足![]() 对一切
对一切![]() 恒成立,则称
恒成立,则称![]() 为“可控数列”.
为“可控数列”.
(1) 若数列![]() 的通项公式为
的通项公式为![]() ,试判断数列
,试判断数列![]() 是否为“可控数列”?并说明理由;
是否为“可控数列”?并说明理由;
(2) 若![]() 是首项为5的“可控数列”,且单调递减,问是否存在常数
是首项为5的“可控数列”,且单调递减,问是否存在常数![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3) 若“可控数列”![]() 的首项为2,
的首项为2,![]() ,求
,求![]() 不同取值的个数及最大值.(直接写出结果)
不同取值的个数及最大值.(直接写出结果)
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)根据所给的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?附:独立检验临界值表
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某书店共有韩寒的图书6种,其中价格为25元的有2种,18元的有3种,16元的有1种.书店若把这6种韩寒的图书打包出售,据统计每套的售价与每天的销售数量如下表所示:
售价x/元 | 105 | 108 | 110 | 112 |
销售数量y/套 | 40 | 30 | 25 | 15 |
(1)根据上表,利用最小二乘法得到回归直线方程![]() ,求
,求![]() ;
;
(2)若售价为100元,则每天销售的套数约为多少(结果保留到整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的函数,它的图象关于点(1,0)对称,当x≤1时,f(x)=2xe﹣x(e为自然对数的底数),则f(2+3ln2)的值为( )
A.48ln2
B.40ln2
C.32ln2
D.24ln2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z1=(a2-4sin2θ)+(1+2cos θ)i,a∈R,θ∈(0,π),z2在复平面内对应的点在第一象限,且z=-3+4i.
(1)求z2及|z2|.
(2)若z1=z2,求θ与a2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系,下表记录了小张某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小张这![]() 天的平均投篮命中率;
天的平均投篮命中率;
(2)利用所给数据求小张每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的线性回归方程
之间的线性回归方程![]() ;(参考公式:
;(参考公式:![]() )
)
(3)用线性回归分析的方法,预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
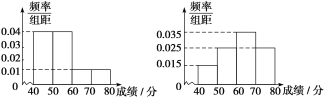
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线
,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线 ![]() 相切.
相切.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点F1、斜率为k1的直线l1与椭圆E交于A,B两点,过点F2、斜率为k2的直线l2与椭圆E交于C,D两点,且直线l1 , l2相交于点P,若直线OA,OB,OC,OD的斜率kOA , kOB , kOC , kOD满足kOA+kOB=kOC+kOD , 求证:动点P在定椭圆上,并求出此椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com