
| A�� | $\frac{152}{75}$ | B�� | $\frac{14}{9}$ | C�� | $\frac{12}{5}$ | D�� | $\frac{3}{2}$ |
���� ��Ȳ�����{an}��{bn}��ǰn��ͷֱ�ΪSn��Tn������֪�ã�$\frac{{S}_{n}}{{T}_{n}}=\frac{4n+6}{n+7}$�����$\frac{{a}_{8}}{{b}_{8}}$�����ɵȲ����е�ͨ�ʽ�����ʿɵ�$\frac{{a}_{3}+{a}_{6}+{a}_{9}+{a}_{14}}{{b}_{3}+{b}_{6}+{b}_{7}+{b}_{11}+{b}_{13}}$=$\frac{4}{5}\frac{{a}_{8}}{{b}_{8}}$��ô𰸣�
��� �⣺��Ȳ�����{an}��{bn}��ǰn��ͷֱ�ΪSn��Tn��
��$\frac{{a}_{1}+{a}_{2}+��+{a}_{n}}{{b}_{1}+{b}_{2}+��{b}_{n}}$=$\frac{4n+6}{n+7}$��n��N*������$\frac{{S}_{n}}{{T}_{n}}=\frac{4n+6}{n+7}$��
��$\frac{{a}_{8}}{{b}_{8}}=\frac{15{a}_{8}}{15{b}_{8}}=\frac{{S}_{15}}{{T}_{15}}=\frac{4��15+6}{15+7}=\frac{66}{22}=3$��
��$\frac{{a}_{3}+{a}_{6}+{a}_{9}+{a}_{14}}{{b}_{3}+{b}_{6}+{b}_{7}+{b}_{11}+{b}_{13}}$=$\frac{4{a}_{1}+28{d}_{1}}{5{b}_{1}+35{d}_{2}}=\frac{4}{5}\frac{{a}_{8}}{{b}_{8}}=\frac{4}{5}��3=\frac{12}{5}$��
��ѡ��C��
���� ���⿼��Ȳ����е�ͨ�ʽ�������˵Ȳ����е����ʣ���������ѧת��˼�뷽�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
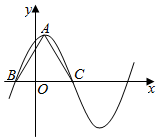 ����f��x��=6cos2$\frac{��x}{2}$+$\sqrt{3}$sin��x-3���أ�0����һ�������ڵ�ͼ����ͼ��ʾ��AΪͼ�����ߵ㣬B��CΪͼ����x��Ľ��㣬�ҡ�ABCΪ�������Σ����=$\frac{��}{4}$��
����f��x��=6cos2$\frac{��x}{2}$+$\sqrt{3}$sin��x-3���أ�0����һ�������ڵ�ͼ����ͼ��ʾ��AΪͼ�����ߵ㣬B��CΪͼ����x��Ľ��㣬�ҡ�ABCΪ�������Σ����=$\frac{��}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-2��-1��0��1} | B�� | {-1��0��1} | C�� | {0��1} | D�� | {1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$+$\frac{4}{3}$ | B�� | $\frac{��}{2}$+3 | C�� | $\frac{��}{4}$+$\frac{4}{3}$ | D�� | $\frac{��}{4}$+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\frac{2}{7}$ | C�� | $\frac{3}{7}$ | D�� | $\frac{4}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com