
分析 (Ⅰ)利用换元法,结合基本不等式,即可求ab的最小值;
(Ⅱ)化二元为一元,利用基本不等式求a+2b的最小值.
解答 解:(Ⅰ)$ab=2a+b+2≥2\sqrt{2ab}+2$,设$\sqrt{ab}=t$,所以${t^2}-2\sqrt{2}t-2≥0$,解得$t≥2+\sqrt{2}$,…(4分)
所以ab最小值为$6+4\sqrt{2}$,当b=2a,即$a=\sqrt{2}+1$时取到.…(6分)
(Ⅱ)由题可得$b=\frac{2a+2}{a-1}(a>1)$,
所以$a+2b=a+\frac{4a+4}{a-1}=a-1+\frac{8}{a-1}+5≥4\sqrt{5}+5$,即a+2b最小值为$4\sqrt{5}+5$,…(10分)
当$a-1=\frac{8}{a-1}$,即$a=2\sqrt{2}+1$时取到.…(12分)
点评 本题考查利用基本不等式求最值,考查学生分析解决问题的能力,正确转化是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在 | B. | 椭圆或线段 | C. | 线段 | D. | 椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
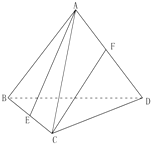 如图,在正四面体ABCD(正四面体是所有棱长都相等的四面体)中,棱长为2,E、F分别为BC、AD的中点.
如图,在正四面体ABCD(正四面体是所有棱长都相等的四面体)中,棱长为2,E、F分别为BC、AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com