
分析 由条件利用两角和的正切公式求得 tan(A+B)=1,可得A+B的值,从而求得C的值,再利用正弦定理求出外接圆的半径.
解答 解:△ABC中,tanA+tanB+tanAtanB=1,
∴tan(A+B)(1-tanAtanB)+tanAtanB=1,
∴tan(A+B)(1-tanAtanB)=1-tanAtanB,
∴tan(A+B)=1,
∴A+B=45°,
∴C=135°;
∴△ABC最大边的长为c=$\sqrt{6}$,
由正弦定理得,2R=$\frac{c}{sinC}$=$\frac{\sqrt{6}}{sin135°}$=$\frac{\sqrt{6}}{\frac{\sqrt{2}}{2}}$=2$\sqrt{3}$,
∴其外接圆的半径为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查两角和的正切公式与正弦定理的应用问题,属于基础题目.


科目:高中数学 来源: 题型:选择题
| A. | [2,10] | B. | [$\sqrt{5}$,$\sqrt{13}$] | C. | [1,5] | D. | [2,$\sqrt{13}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2sin2016 | B. | sin2016 | C. | 0 | D. | 2sin2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{50}$ | B. | $\frac{13}{50}$ | C. | $\frac{37}{50}$ | D. | $\frac{49}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | $\frac{1}{9}$ | D. | $\frac{10}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(-$\frac{π}{8}$)<sin(-$\frac{π}{10}$) | B. | sin(-$\frac{23}{5}π$)$>sin(-\frac{17}{4}π)$ | ||
| C. | sin3>sin2 | D. | sin$\frac{7π}{5}$>sin(-$\frac{2π}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
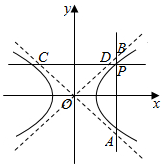 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com