
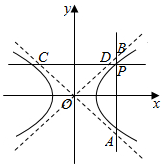
 已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值.
已知P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1上的任意一点,过P作x轴的垂线,分别交双曲线的两条渐近线于A,B两点,过P作y轴的垂线,分别交双曲线的两条渐近线于C,D两点.求证:|PA|•|PB|+|PC|•|PD|为定值. 分析 设P(m,n),可得$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,即为b2m2-a2n2=a2b2,求出双曲线的渐近线方程,令x=m,y=n,分别求得A,B,C,D的坐标,运用两点的距离公式化简整理,即可得证.
解答 证明:设P(m,n),可得$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,
即为b2m2-a2n2=a2b2,
双曲线的渐近线方程为y=±$\frac{b}{a}$x,
由x=m,可得y=±$\frac{bm}{a}$,
即有A(m,$\frac{bm}{a}$),B(m,-$\frac{bm}{a}$),
由y=n,可得x=±$\frac{an}{b}$,
即有C($\frac{an}{b}$,n),D(-$\frac{an}{b}$,n),
可得|PA|•|PB|+|PC|•|PD|=|n-$\frac{bm}{a}$|•|n+$\frac{bm}{a}$|+|m-$\frac{an}{b}$|•|m+$\frac{an}{b}$|
=|n2-$\frac{{b}^{2}{m}^{2}}{{a}^{2}}$|+|m2-$\frac{{a}^{2}{n}^{2}}{{b}^{2}}$|=$\frac{{a}^{2}{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}{b}^{2}}{{b}^{2}}$=a2+b2.即为定值.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题为:“若x=a且x=b,则x2-(a+b)x+ab=0” | |
| B. | “x=-1”是“x2-5x-6=0”的根的逆命题是真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{3}{4},+∞)$ | C. | $(\frac{1}{2},+∞)$ | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com