Question

8．设$f（x）={e^{\frac{1}{2}x}}$（x-1）-ax+2a恰有小于1两个零点，则a的取值范围是（　　）

• A． $（0，\frac{1}{2}）$
• B． $（0，\frac{2}{{3\sqrt{e}}}）$
• C． $（-∞，\frac{1}{2}]$
• D． $（-∞，\frac{2}{{3\sqrt{e}}}]$

Answer 1

分析 令f（x）=0，使用分离参数法得a=$\frac{{e}^{\frac{1}{2}x}（x-1）}{x-2}$，则令g（x）=$\frac{{e}^{\frac{1}{2}x}（x-1）}{x-2}$，求出g（x）在（-∞，1）上的值域．则根据a=g（x）有两解得出a的范围．

解答 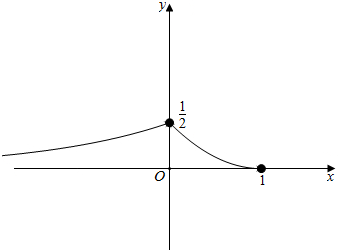解：令f（x）=0得e${\;}^{\frac{1}{2}x}$（x-1）=ax-2a，∴a=$\frac{{e}^{\frac{1}{2}x}（x-1）}{x-2}$．令g（x）=$\frac{{e}^{\frac{1}{2}x}（x-1）}{x-2}$．则g′（x）=$\frac{（\frac{1}{2}{e}^{\frac{1}{2}x}（x-1）+{e}^{\frac{1}{2}x}）（x-2）-{e}^{\frac{1}{2}x}（x-1）}{（x-2）^{2}}$=e${\;}^{\frac{1}{2}x}$$•\frac{x}{2（x-2）^{2}}$•（x-3）．
令g′（x）=0，得x=0或x=3．
当x＜0时，g′（x）＞0，当0＜x≤1时，g′（x）＜0，∴g（x）在（-∞，0）上是增函数，在（0，1]上是减函数，
∵$\underset{lim}{n→-∞}g（x）=0$，g（0）=$\frac{1}{2}$，g（1）=0，∴g（x）在（-∞，1）上的值域为（0，$\frac{1}{2}$]．
作出g（x）在（-∞，1）上函数的大致图象如图：
∵$f（x）={e^{\frac{1}{2}x}}$（x-1）-ax+2a恰有小于1两个零点，∴a=g（x）在（-∞，1）上有两解．
∴0＜a$＜\frac{1}{2}$．
故选A．

点评 本题考查了函数的单调性，函数的值域，零点的个数判断，借助函数图象可比较方便的得出结论．