
| an | bn | an•bn | 判断{an•bn}是否是等比数列 | |
| 例 | 3×($\frac{2}{3}$)n | -5×2n-1 | -10×($\frac{4}{3}$)n-1 | 是 |
| 自选1 | ||||
| 自选2 |
分析 利用等比数列的通项与定义,即可得出结论.
解答 解:由题意,
| an | bn | an•bn | 判断{an•bn}是否是等比数列 | |
| 例 | 3×($\frac{2}{3}$)n | -5×2n-1 | -10×($\frac{4}{3}$)n-1 | 是 |
| 自选1 | 4×($\frac{2}{3}$)n | -5×4n-1 | -5×($\frac{8}{3}$)n | 是 |
| 自选2 | 3×($\frac{2}{3}$)n | 5×2n-1 | 10×($\frac{4}{3}$)n-1 | 是 |
点评 本题考查等比数列的通项与定义,考查学生 的计算能力,比较基础.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x1-(a+bx1)|+|x2-(a+bx2)|+|x3-(a+bx3)| | B. | [x1-(a+bx1)]2+[x2-(a+bx2)]2+[x3-(a+bx3)]2 | ||
| C. | |y1-(a+bx1)|+|y2-(a+bx2)|+|y3-(a+bx3)| | D. | [y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
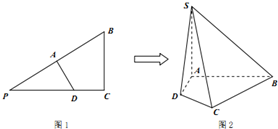 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com