
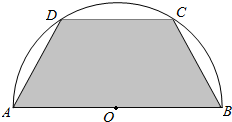
 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.分析 (1)过点C作CE⊥AB,垂足为E,因为∠BOC=θ(0<θ<$\frac{π}{2}$),OC=1,从而写出OE=cosθ,CE=sinθ,从而可得y=$\frac{1}{2}$(AB+CD)CE=$\frac{1}{2}$(2+2cosθ)sinθ=(1+cosθ)sinθ,(0<θ<$\frac{π}{2}$);
(2)求导y′=(sinθ+sinθcosθ)′=2cos2θ+cosθ-1,由导数的正负确定函数的单调性,从而求最大值.
解答 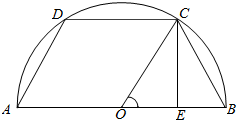 解:(1)过点C作CE⊥AB,垂足为E,因为∠BOC=θ(0<θ<$\frac{π}{2}$),OC=1,
解:(1)过点C作CE⊥AB,垂足为E,因为∠BOC=θ(0<θ<$\frac{π}{2}$),OC=1,
所以OE=cosθ,CE=sinθ,
所以y=$\frac{1}{2}$(AB+CD)CE=$\frac{1}{2}$(2+2cosθ)sinθ=(1+cosθ)sinθ,(0<θ<$\frac{π}{2}$);
(2)y′=(sinθ+sinθcosθ)′=2cos2θ+cosθ-1,
令y′=0得cosθ=$\frac{1}{2}$,即θ=$\frac{π}{3}$,cosθ=-1(舍),
所以当0<θ<$\frac{π}{3}$时,y′>0,所以函数在(0,$\frac{π}{3}$)上单调递增,
当$\frac{π}{3}$<θ<$\frac{π}{2}$时,y′<0,所以函数在($\frac{π}{3}$,$\frac{π}{2}$)上单调递减;
所以当θ=$\frac{π}{3}$时,ymax=$\frac{3\sqrt{3}}{4}$.
答:梯形部件ABCD面积的最大值为$\frac{3\sqrt{3}}{4}$平方米.
点评 本题考查了导数的综合应用及函数在实际问题中的应用,同时考查了三角函数的化简与应用,属于中档题.


科目:高中数学 来源: 题型:填空题
 中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点,左右焦点分别为F1、F2,且它们在第一象限的交点为P,△PF1F2是以PF2为底边的等腰三角形.若|PF2|=10,双曲线离心率的取值范围为(1,2),则椭圆离心率的取值范围是($\frac{2}{3}$,1).
中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点,左右焦点分别为F1、F2,且它们在第一象限的交点为P,△PF1F2是以PF2为底边的等腰三角形.若|PF2|=10,双曲线离心率的取值范围为(1,2),则椭圆离心率的取值范围是($\frac{2}{3}$,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 12 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com