
 中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点,左右焦点分别为F1、F2,且它们在第一象限的交点为P,△PF1F2是以PF2为底边的等腰三角形.若|PF2|=10,双曲线离心率的取值范围为(1,2),则椭圆离心率的取值范围是($\frac{2}{3}$,1).
中心在原点、焦点在x轴上的椭圆与双曲线有公共焦点,左右焦点分别为F1、F2,且它们在第一象限的交点为P,△PF1F2是以PF2为底边的等腰三角形.若|PF2|=10,双曲线离心率的取值范围为(1,2),则椭圆离心率的取值范围是($\frac{2}{3}$,1). 分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为e1,双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m>0,n>0,离心率为e2,|F1F2|=2c,由e1=$\frac{c}{a}$,e2=$\frac{c}{m}$∈(1,2),由△PF1F2是以PF2为底边的等腰三角形,结合椭圆与双曲线的定义可求得a=c+5,m=c-5,由不等式的解法,从而可求得答案.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为e1,
双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m>0,n>0),|F1F2|=2c,
∵有公共焦点的椭圆与双曲线在第一象限的交点为P,
△PF1F2是以PF2为底边的等腰三角形,|PF2|=10,
∴在椭圆中,|PF1|+|PF2|=2a,而|PF1|=|F1F2|=2c,
∴|PF2|=2a-2c;①
同理,在该双曲线中,|PF2|=-2m+2c;②
由①②可得m=c-5,a=c+5.
∵e2=$\frac{c}{m}$∈(1,2),即1<$\frac{c}{c-5}$<2,
∴c>10,
又e1=$\frac{c}{a}$=$\frac{c}{c+5}$=1-$\frac{5}{c+5}$,0<$\frac{5}{c+5}$<$\frac{1}{3}$
由c>10,可得0<$\frac{5}{c+5}$<$\frac{1}{3}$,
即有$\frac{2}{3}$<e1<1.
故答案为:($\frac{2}{3}$,1).
点评 本题考查椭圆与双曲线的简单性质:离心率的范围,考查等价转换的思想与运算能力,考查不等式的解法,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ① | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
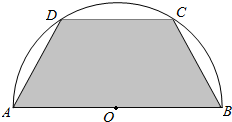 如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截去一个内接等腰梯形部件ABCD,设梯形ABCD的面积为y平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com