练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知命题p：?x0∈R，x0-2＞0，命题q：?x∈R，$\sqrt{x}$＜x，则下列说法中正确的是（　　）
    A．命题p∨q是假命题B．命题p∧q是真命题
    C．命题p∧（￢q）是真命题D．命题p∨（￢q）是假命题

    分析 先判断命题p，q的真假，进而根据复合命题真假判断的真值表，得到答案．

    解答 解：?x0=3∈R，x0-2＞0，故命题p为真命题；
    当x∈[0，1]时，$\sqrt{x}$≥x，故命题q为假命题，
    故命题p∨q是真命题，
    命题p∧q是假命题，
    命题p∧（￢q）是真命题，
    命题p∨（￢q）是真命题，
    故选：C．

    点评 本题以命题的真假判断与应用为载体，考查了复合命题，全称命题，特称命题等知识点，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．半径为2，圆心角为36°的扇形的面积是$\frac{2}{5}$π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知点A（1，1）和点B（-1，-3）在曲线C：y=ax3+bx2+d（a，b，d为常数），若曲线在点A和点B处的切线互相平行，则a+b+d=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设f（x）=$\left\{\begin{array}{l}{{k}^{2}x+{a}^{2}-k（x≥0）}\\{{x}^{2}+（{a}^{2}+4a）x+（2-a）^{2}（x＜0）}\end{array}\right.$，其中a∈R，若对任意的非零实数x1，存在唯一的非零实数x2（x1≠x2），使得f（x2）=f（x1）成立，则k的取值范围为（　　）
    A．[-20，-4]B．[-30，-9]C．[-4，0]D．[-9，-4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．设函数f（x）=xea-x+bx，曲线y=f（x）在点（2，f（2））处的切线方程为y=（e-1）x+4．
    （1）求a，b的值；    
    （2）求f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

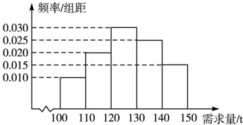    12．经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130t该农产品．以X（单位：t，100≤X≤150）表示下一个销售季度内的市场需求量，T（单位：元）表示下一个销售季度内经销该农产品的利润．
    （I）将T表示为X的函数；
    （II）根据直方图求利润T不少于57 000元的频率；
    （Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值 （例如：若需求量X∈[100，110），则取X=105），估计T的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量，$\overrightarrow{a}$=（1，m），$\overrightarrow{b}$=（3，-2），且（$\overrightarrow{a}$+$\overrightarrow{b}$）∥$\overrightarrow{b}$，则m=（　　）
    A．$-\frac{2}{3}$B．$\frac{2}{3}$C．-8D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若R上的可导函数f（x）满足f（x）=x2-xf'（1）+1，则f'（0）=（　　）
    A．-2B．-1C．0D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．函数f（x）=x-$\frac{1}{x}$的图象关于（　　）
    A．y轴对称B．直线y=x对称C．坐标原点对称D．直线y=-x对称

    查看答案和解析>>

    同步练习册答案