
| A. | y2=4x | B. | y2=-4x | C. | y2=8x | D. | y2=-8x |
分析 由抛物线的对称性知,AB⊥x轴,且AB是焦点弦,故AB=2p,利用△KAB的面积为24,求出p的值,求得直线AB的方程,即可求得以直线AB为准线的抛物线标准方程.
解答 解:由抛物线的对称性知,AB⊥x轴,且AB是焦点弦,故丨AB丨=2p,
∴△CAB的面积S=$\frac{1}{2}$×丨AB丨×d=$\frac{1}{2}$×2p×($\frac{p}{2}$+4)=24,整理得:p2+8p-48=0,
解得p=4,或p=-12(舍去),
∴p=4,则抛物线方程y2=8x,
∴AB的方程:x=2,
∴以直线AB为准线的抛物线标准方程y2=-8x,
故选D.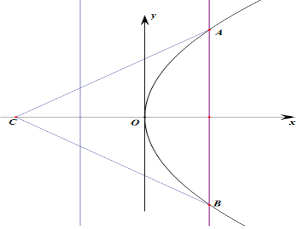
点评 本题考查三角形面积的计算,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 0 | C. | 5 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4) | B. | (0,$\frac{4}{3}$) | C. | (0,2) | D. | ($\frac{4}{3}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》中记载了一种标准量器---商鞅铜方升,其三视图如图所示(单位:寸),则该几何体的容积为( )立方寸.(π≈3.14)
《九章算术》中记载了一种标准量器---商鞅铜方升,其三视图如图所示(单位:寸),则该几何体的容积为( )立方寸.(π≈3.14)| A. | 12.656 | B. | 13.667 | C. | 11.414 | D. | 14.354 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com