
分析 (I)设等比数列{an}的公比为q>0,由2a5,a4,4a6成等差数列,可得2a4=2a5+4a6,化为:2q2+q-1=0,q>0,解得q.又满足a4=4a32,化为:1=4a1q,解得a1.可得an.
(II)bn=$\frac{{a}_{n+1}}{(1-{a}_{n})(1-{a}_{n+1})}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$,n∈N*,利用“裂项求和”方法即可得出.
解答 解:(I)设等比数列{an}的公比为q>0,∵2a5,a4,4a6成等差数列,∴2a4=2a5+4a6,∴2a4=2a4(q+2q2),
化为:2q2+q-1=0,q>0,解得q=$\frac{1}{2}$.
又满足a4=4a32,∴${a}_{1}{q}^{3}$=4$({a}_{1}{q}^{2})^{2}$,化为:1=4a1q,解得a1=$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n}$(n∈N*),.
(II)bn=$\frac{{a}_{n+1}}{(1-{a}_{n})(1-{a}_{n+1})}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$,n∈N*,
∴数列{bn}的前n项和Sn=$(\frac{1}{2-1}-\frac{1}{{2}^{2}-1})$+$(\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1})$+…+$(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$
=1-$\frac{1}{{2}^{n+1}-1}$=$\frac{{2}^{n+1}-2}{{2}^{n+1}-1}$,n∈N*.
点评 本题考查了“裂项求和”方法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
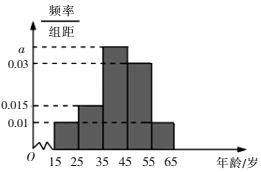 2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题时百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示.
2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题时百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
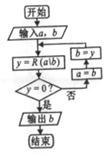 我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )
我国古代数学名著《九章算术》中的更相减损术的算法思路与右图类似.记R(a\b)为a除以b所得的余数(a,b∈N*),执行程序框图,若输入a,b分别为266,63,则输出的b的值为( )| A. | 1 | B. | 3 | C. | 7 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | 22 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {k|k≤-1或k≥1} | B. | {k|-1<k<1} | C. | {k|k<-1} | D. | {k|k≤-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com