
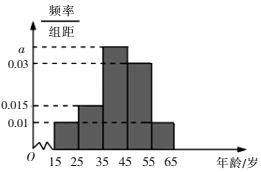
 2017�곻���������ٿ�ǰϦ��ij��վ�Ƴ������ȵ���͵��飬�������ݱ�������������ʱ������Ϊ���ĵ��ȵ㣬����������й�ע�������Լռ80%���ִӲ����������ѡ��200�ˣ�������200�˰�������飺��1��[15��25������2��[25��35������3��[35��45������4��[45��55������5��[55��65�����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
2017�곻���������ٿ�ǰϦ��ij��վ�Ƴ������ȵ���͵��飬�������ݱ�������������ʱ������Ϊ���ĵ��ȵ㣬����������й�ע�������Լռ80%���ִӲ����������ѡ��200�ˣ�������200�˰�������飺��1��[15��25������2��[25��35������3��[35��45������4��[45��55������5��[55��65�����õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������ ��1����Ƶ�ʷֲ�ֱ��ͼ��С���ε����֮��Ϊ1�������a��
��2���ֲ�����ķ����ڵ�3����Ӧ��ȡ7�ˣ����¼�����ȡ3����������1�������ڵ�3�顱ΪA����$\overline{A}$Ϊ����ȡ��3����û��1�������е�3�顱���ɴ��������ȡ��3����������1�˵������ڵ�3��ĸ��ʣ�
��3��X�����п���ֵΪ0��1��2��3���������X��B��3��$\frac{4}{5}$�����ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ã�
��0.01+0.015+0.03+a+0.01����10=1��
���a=0.035��
��2���ֲ�����ķ����ڵ�3����Ӧ��ȡ$\frac{0.035}{0.01+0.015+0.035}��12$=7�ˣ�
���¼�����ȡ3����������1�������ڵ�3�顱ΪA��
��$\overline{A}$Ϊ����ȡ��3����û��1�������е�3�顱��
���ȡ��3����������1�˵������ڵ�3��ĸ��ʣ�
P��A��=1-P��$\overline{A}$��=1-$\frac{{C}_{5}^{3}}{{C}_{12}^{3}}$=$\frac{21}{22}$��
��3��X�����п���ֵΪ0��1��2��3���������X��B��3��$\frac{4}{5}$����
��P��X=k��=${C}_{3}^{k}��\frac{4}{5}��^{k}��\frac{1}{5}��^{3-k}$��k=0��1��2��3��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{125}$ | $\frac{12}{125}$ | $\frac{48}{125}$ | $\frac{64}{125}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�������¼����ʳ˷���ʽ������ֲ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��0�� | B�� | ��0��3�� | C�� | {0��3} | D�� | {3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��+�ޣ� | B�� | $[{\frac{1}{2}��1}]$ | C�� | $[{\frac{2}{3}��+��}��$ | D�� | ��1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | �ܼ� | |
| �װ� | 10 | ||
| �Ұ� | 30 | ||
| �ϼ� | 100 |
| P��K2��k�� | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}$ | B�� | $2\sqrt{2}$ | C�� | $2\sqrt{3}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��-�ޣ�3�� | C�� | ��-2��1�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com