练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．已知A=[1，+∞），$B=\left\{{x∈R|\frac{1}{2}≤x≤2a-1}\right\}$，若A∩B≠∅，则实数a的取值范围是（　　）
    A．[1，+∞）B．$[{\frac{1}{2}，1}]$C．$[{\frac{2}{3}，+∞}）$D．（1，+∞）

    分析 根据A与B的交集不为空集，求出a的范围即可．

    解答 解：A=[1，+∞），$B=\left\{{x∈R|\frac{1}{2}≤x≤2a-1}\right\}$，且A∩B≠∅，
    ∴2a-1≥1，
    ∴a≥1，
    故选：A．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

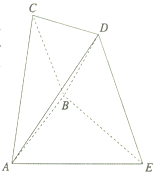    15．在如图所示的空间几何体中，边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直，DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°，DE=2．
    （Ⅰ）求证：CD⊥平面ABC；
    （Ⅱ）求二面角A-BE-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若f（x）+3f（-x）=log2（x+3），则f（1）=$\frac{1}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．拖延症总是表现在各种小事上，但日积月累，特别影响个人发展，某校的一个社会实践调查小组，在对该校学生进行“是否有明显拖延症”的调查中，随机发放了110份问卷．对收回的100份有效问卷进行统计，得到如下2×2列联表：
    有明显拖延症无明显拖延症合计
    男352560
    女301040
    总计6535100
    （Ⅰ）按女生是否有明显拖延症进行分层，已经从40份女生问卷中抽取了8份问卷，现从这8份问卷中再随机抽取3份，并记其中无明显拖延症的问卷的份数为X，试求随机变量X的分布列和数学期望；
    （2）若在犯错误的概率不超过P的前提下认为无明显拖延症与性别有关，那么根据临界值表，最精确的P的值应为多少？请说明理由
    附：独立性检验统计量K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d 
    P（K2≥k0）0.250.150.100.050.025
    k01.3232.0722.7063.8415.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知正项等差数列{an}的前n项和为Sn，S10=40，则a3•a8的最大值为16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．在${（{x-\frac{1}{x}-1}）^4}$的展开式中，常数项为-5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．清代著名数学家梅彀成在他的《增删算法统宗》中有这样一歌谣：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”其译文为：“远远望见7层高的古塔，每层塔点着的灯数，下层比上层成倍地增加，一共有381盏，请问塔尖几盏灯？”则按此塔各层灯盏的设置规律，从上往下数第4层的灯盏数应为（　　）
    A．3B．12C．24D．36

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

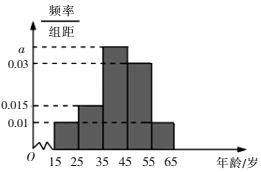    14．2017年郴州市两会召开前夕，某网站推出两会热点大型调查，调查数据表明，民生问题时百姓最为关心的热点，参与调查者中关注此问题的约占80%，现从参与者中随机选出200人，并将这200人按年龄分组：第1组[15，25），第2组[25，35），第3组[35，45），第4组[45，55），第5组[55，65），得到的频率分布直方图如图所示．
    （1）求出频率分布直方图中的a值，并求出这200的平均年龄；
    （2）现在要从年龄较小的第1，2，3组用分层抽样的方法抽取12人，再从这12人中随机抽取3人赠送礼品，求抽取的3人中至少有1人的年龄在第3组的概率；
    （3）若要从所有参与调查的人（人数很多）中随机选出3人，记关注民生问题的人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知数列{an}的前n项和为${S_n}=5{n^2}+10n$，（其中n∈N*），则a3=35．

    查看答案和解析>>

    同步练习册答案