Question

9．一位同学家里订了一份报纸，送报人每天早上6：20-7：40之间将报纸送达，该同学需要早上7：00-8：00之间出发上学，则这位同学在离开家之前能拿到报纸的概率为（　　）

• A． $\frac{1}{6}$
• B． $\frac{1}{3}$
• C． $\frac{2}{3}$
• D． $\frac{5}{6}$

Answer 1

分析 设送报人到达的时间为x，这位同学在离开家为y，（x，y）可以看成平面中的点，
利用图形表示出事件所构成的区域，利用面积比求出对应的概率值．

解答 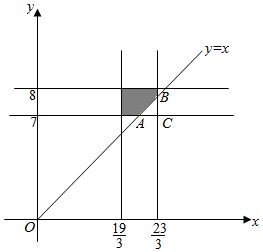解：如图所示，设送报人到达的时间为x，这位同学在离开家为y；
则（x，y）可以看成平面中的点，试验的全部结果所构成的区域为
Ω={（x，y）|$\frac{19}{3}$≤x≤$\frac{23}{3}$，且7≤y≤8}，
其矩形区域的面积为S_Ω=（$\frac{23}{3}$-$\frac{19}{3}$）×（8-7）=$\frac{4}{3}$；
事件A所构成的区域为
A={（x，y）|$\frac{19}{3}$≤x≤$\frac{23}{3}$，且7≤y≤8，且x≤y}，
即图中的阴影部分，
其中A（7，7），C（$\frac{23}{3}$，7），B（$\frac{23}{3}$，$\frac{23}{3}$），
且△ABC的面积为S′=$\frac{1}{2}$×（$\frac{23}{3}$-7）×（$\frac{23}{3}$-7）=$\frac{2}{9}$，
则阴影部分的面积为S_A=$\frac{4}{3}$-$\frac{2}{9}$=$\frac{10}{9}$．
所求对应的概率为P=$\frac{\frac{10}{9}}{\frac{4}{3}}$=$\frac{5}{6}$．
故选：D．

点评 本题考查了几何概型的概率计算问题，也考查了二元一次不等式组表示平面区域的问题，是中档题．