
| A. | $(1,\frac{3}{2})$ | B. | $({\frac{3}{2},+∞}]$ | C. | (1,2] | D. | [2,+∞) |
分析 由已知可得函数$y={log_a}({x^2}-ax+\frac{1}{2})$在区间[1,+∞)上为增函数,结合二次函数,指数函数和复合函数的单调性,可得答案.
解答 解:若对任意的x1,x2∈[1,+∞),且x1≠x2时,满足$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0$,
则函数$y={log_a}({x^2}-ax+\frac{1}{2})$在区间[1,+∞)上为增函数,
由t=${x}^{2}-ax+\frac{1}{2}$在[$\frac{a}{2}$,+∞)上为增函数,
故$\left\{\begin{array}{l}a>1\\ \frac{a}{2}≤1\\ 1-a+\frac{1}{2}>0\end{array}\right.$,
解得:a∈$(1,\frac{3}{2})$,
故选:A.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
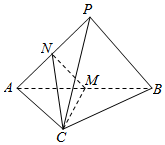 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{BC}$ | B. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$ | C. | $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{CB}$ | D. | $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥$\frac{1}{2}$ | B. | k≤-2 | C. | k≥$\frac{1}{2}$或k≤-2 | D. | -2≤k≤$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com