
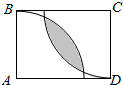
 如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.
如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$. 分析 以AD所在直线为x轴,AB所在直线为y轴,建立坐标系,求出公共弦的方程,圆心A到直线的距离d=$\frac{3}{\sqrt{8+4}}$=$\frac{\sqrt{3}}{2}$,可得阴影部分弧所对的圆心角,即可求出点落在阴影部分内的概率.
解答 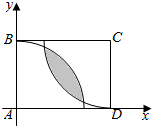 解:以AD所在直线为x轴,AB所在直线为y轴,建立坐标系,则
解:以AD所在直线为x轴,AB所在直线为y轴,建立坐标系,则
圆A的方程为x2+y2=1,圆C的方程为(x-$\sqrt{2}$)2+(y-1)2=1,
两方程相减可得2$\sqrt{2}$x+2y-3=0,
圆心A到直线的距离d=$\frac{3}{\sqrt{8+4}}$=$\frac{\sqrt{3}}{2}$,∴阴影部分弧所对的圆心角为$\frac{π}{3}$,
∴S阴影=2($\frac{π}{6}$-$\frac{\sqrt{3}}{4}$)=$\frac{π}{3}$-$\frac{\sqrt{3}}{2}$,
∵矩形的面积为$\sqrt{2}$,
∴该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.
故答案为:$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$
点评 本题考查几何概型,考查学生的计算能力,确定阴影部分的面积是关键.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com