
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,即可判断出正误;
②利用非命题的定义即可判断出正误;
③对于实数a,b,“b<a<0”⇒“$\frac{1}{b}$>$\frac{1}{a}$”,反之不成立,例如取a>b>0时,$\frac{1}{b}$>$\frac{1}{a}$,即可判断出正误;
④由已知可得:可得命题p是假命题,q一定是真命题,即可判断出正误.
解答 解:①命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,因此不正确;
②命题p:“?x∈(-∞,0),2x<3x”,则¬p:“?x∈(-∞,0),2x≥3x”,不正确;
③对于实数a,b,“b<a<0”⇒“$\frac{1}{b}$>$\frac{1}{a}$”,反之不成立,例如取a>b>0时,$\frac{1}{b}$>$\frac{1}{a}$,因此,“b<a<0”是“$\frac{1}{b}$>$\frac{1}{a}$”成立的充分不必要条件,正确;
④如果命题“¬p”与命题“p或q”都是真命题,那么命题p是假命题,q一定是真命题,正确.
综上可得:正确的命题个数为2.
故选:B.
点评 本题考查了简易逻辑的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
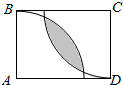 如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.
如图在矩形ABCD,AB=1,AD=$\sqrt{2}$,在矩形区域内任取一点P,使得该点落在阴影部分内的概率为$\frac{\sqrt{2}π}{6}-\frac{\sqrt{6}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{4}$ | B. | $\frac{15}{2}$ | C. | $\frac{7}{4}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$i | D. | $\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 4 | 1 | 3 | 5 | 2 |
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com